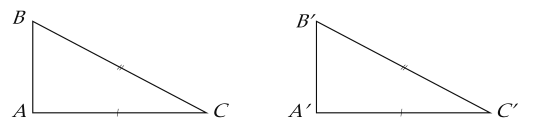Bài học cùng chủ đề
Các trường hợp bằng nhau của tam giác vuông. SVIP
1. Ba trường hợp bằng nhau của tam giác vuông
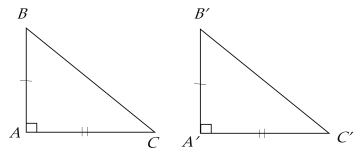
a. Trường hợp 1
Nếu hai cạnh góc vuông của tam giác này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác đó bằng nhau.
Ta có thể trình bày định lí dưới dạng giả thiết - kết luận như sau:
Giả thiết | $\widehat{BAC} = \widehat{B'A'C'} = 90^\circ$, $AB = A'B'$, $AC = A'C'$ |
Kết luận | $\Delta ABC = \Delta A'B'C'$ |
Ví dụ 1. Cho hình vẽ sau:
Chứng minh rằng $\Delta ABH=\Delta ACH$.
Lời giải
Xét $\Delta ABH$ và $\Delta ACH$ có:
$BH=CH$ (giả thiết);
$\widehat{AHB}=\widehat{AHC}=90^\circ$;
$AH$: cạnh chung.
Suy ra $\Delta ABH=\Delta ACH$ (c.g.c).
Câu hỏi:
@205140494731@
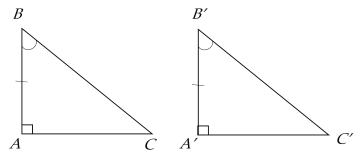
b. Trường hợp 2
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ta có thể trình bày định lí dưới dạng giả thiết - kết luận như sau:
Giả thiết | $\widehat{BAC} = \widehat{B'A'C'} = 90^\circ$, $AB = A'B'$, $\widehat{ABC} = \widehat{A'B'C'}$ |
Kết luận | $\Delta ABC = \Delta A'B'C'$ |
Ví dụ 2. Cho hình vẽ sau:
Chứng minh rằng $\Delta ABH=\Delta ACH$.
Lời giải
Xét $\Delta ABH$ và $\Delta ACH$ có:
$\widehat{BAH}=\widehat{CAH}$ (giả thiết);
$AH$: cạnh chung;
$\widehat{AHB}=\widehat{AHC}=90^\circ$.
Suy ra $\Delta ABH=\Delta ACH$ (g.c.g).
Câu hỏi:
@205141846962@
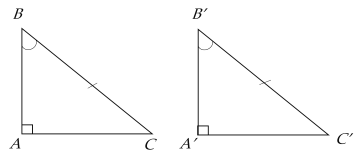
c. Trường hợp 3
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác đó bằng nhau.
Ta có thể trình bày định lí dưới dạng giả thiết - kết luận như sau:
Giả thiết | $\widehat{BAC} = \widehat{B'A'C'} = 90^\circ$, $BC = B'C'$, $\widehat{ABC} = \widehat{A'B'C'}$ |
Kết luận | $\Delta ABC = \Delta A'B'C'$ |
Ví dụ 3. Cho hình vẽ sau:
Chứng minh rằng $\Delta XYZ=\Delta XTZ$.
Lời giải
Xét hai tam giác vuông $\Delta XYZ$ và $\Delta XTZ$ có:
$\widehat{YXZ}=\widehat{TXZ}$ (giả thiết);
$XZ$: cạnh chung.
Suy ra $\Delta XYZ=\Delta XTZ$ (cạnh huyền-góc nhọn).
Câu hỏi:
@202502536745@
2. Trường hợp bằng nhau đặc biệt của tam giác vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ta có thể trình bày định lí dưới dạng giả thiết - kết luận như sau:
Giả thiết | $\widehat{BAC} = \widehat{B'A'C'} = 90^\circ$, $AC = A'C'$, $BC = B'C'$ |
Kết luận | $\Delta ABC = \Delta A'B'C'$ |
Ví dụ 3. Cho hình vẽ sau:
Chứng minh rằng $\Delta ABC=\Delta ADC$.
Lời giải
Xét hai tam giác vuông $\Delta ABC$ và $\Delta ADC$ có:
$AB=AD$ (giả thiết);
$AC$: cạnh chung.
Suy ra $\Delta ABC=\Delta ADC$ (cạnh huyền-cạnh góc vuông).
Câu hỏi:
@205142435131@