Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra cuối học kì I - lớp 12 bộ sách Kết nối tri thức SVIP

Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Hàm số y=x3−3x2+4 đồng biến trên mỗi khoảng nào sau đây?
Cho hàm số y=f(x) có đồ thị như hình vẽ sau:

Điểm cực đại của đồ thị hàm số đã cho là
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y=x−1−2x−1 có phương trình lần lượt là
Cho hình lập phương ABCD.A′B′C′D′. Gọi O là tâm của hình lập phương. Khẳng định nào sau đây là đúng?
Trong không gian Oxyz, cho vectơ a được biểu diễn bởi các vectơ đơn vị là a=2i+k−3j. Tọa độ của vectơ a là
Cho bảng biểu diễn mẫu số liệu ghép nhóm về việc theo dõi cân nặng của 45 em học sinh lớp 1 tại trường Tiểu học ở địa phương cho kết quả sau:
Cân nặng (kg) | Số học sinh |
[16;21) | 11 |
[21;26) | 21 |
[26;31) | 8 |
[31;36) | 5 |
Khoảng biến thiên R cho mẫu số liệu ghép nhóm trên bằng
Gọi Q1,Q2,Q3 là tứ phân vị của một mẫu số liệu ghép nhóm. Khi đó khoảng tứ phân vị ΔQ của mẫu số liệu trên được xác định bởi công thức là
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1+2;2;1−2). Tọa độ điểm M′∈(Oyz) sao cho độ dài đoạn thẳng MM′ ngắn nhất là
Cho hàm số y=cx+dax+b có đồ thị như hình vẽ dưới.
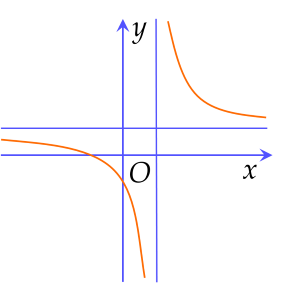
Mệnh đề nào dưới đây đúng?
Tất cả các giá trị thực của tham số để hàm số y=x−mx−2 đồng biến trên khoảng (−∞;1) là
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC có ba đỉnh A(−1;1;−3), B(4;2;1), C(3;0;5). Tọa độ trọng tâm G của tam giác ABC là
Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên:
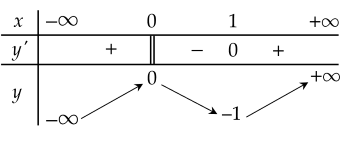
| a) Hàm số có giá trị cực tiểu bằng 1. |
|
| b) Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng −1. |
|
| c) Hàm số đạt cực đại tại x=0 và đạt cực tiểu tại x=1. |
|
| d) Hàm số có đúng một cực trị. |
|
Giá đóng cửa của một cổ phiếu là giá của cổ phiếu đó cuối một phiên giao dịch. Bảng sau thống kê giá đóng cửa của hai mã cổ phiếu A và B trong 50 ngày giao dịch liên tiếp.
Giá đóng cửa | Cổ phiếu A | Cổ phiếu B |
[120;122) | 8 | 16 |
[122;124) | 9 | 4 |
[124;126) | 12 | 3 |
[126;128) | 10 | 6 |
[128;130) | 11 | 21 |
| a) Xét mẫu số liệu của cổ phiếu A ta có phương sai của mẫu số liệu ghép nhóm là 7,5216. |
|
| b) Xét mẫu số liệu của cổ phiếu B ta có số trung bình của mẫu số liệu ghép nhóm là 115,28. |
|
| c) Xét mẫu số liệu của cổ phiếu B ta có độ lệch chuẩn của mẫu số liệu ghép nhóm là 15,4096. |
|
| d) Người ta có thể dùng phương sai và độ lệch chuẩn để so sánh mức độ rủi ro của các loại cổ phiếu có giá trị trung bình gần bằng nhau. Theo quan điểm trên, thì cổ phiếu A có độ rủi ro thấp hơn cổ phiếu B. |
|
Cho hình hộp ABCD.A′B′C′D′
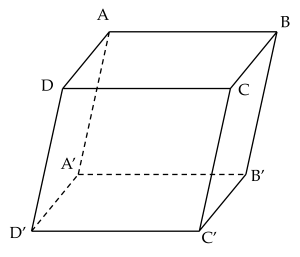
| a) AB′=C′D. |
|
|
b) AB+B′C′+DD′=AC′. |
|
|
c) BD−DD′−B′D′=BB′. |
|
|
d) AC+BA′+DB+C′D=0. |
|
Cho hàm số y=x−2x2−2x+4 có đồ thị (C). Khi đó:
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Tập xác định của hàm số đã cho là R. |
|
| b) Đồ thị hàm số có tiệm cận đứng là đường thẳng x=2 và có tiệm cận xiên là đường thẳng y=x. |
|
| c) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng 4. |
|
| d) Cho đường thẳng y=mx−2. Khi đó có đúng 8 giá trị nguyên của tham số m không vượt quá 10 để đồ thị hàm số đã cho cắt đường thẳng y=mx−2 tại hai điểm phân biệt nằm về hai phía so với tiệm cận đứng của đồ thị (C). |
|
Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hoá bằng hàm số y=f(t)=1+5e−t5000,t≥0, trong đó thời gian t (năm) được tính kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm f′(t) sẽ biểu thị tốc độ bán hàng. Sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất? (làm tròn kết quả tới chữ số hàng phần mười)
Trả lời:
Có bao nhiêu giá trị nguyên của m để hàm số y=x+m2x+1 nghịch biến trên khoảng (3;+∞) ?
Trả lời:
Có bao nhiêu giá trị nguyên của tham số thực m để đường thẳng y=3x+m−2 cắt đồ thị y=(x−1)3 tại ba điểm phân biệt?
Trả lời:
Một hãng dược phẩm dùng những chiếc lọ bằng nhựa có dạng hình trụ để đựng thuốc. Biết rằng mỗi lọ có thể tích là 16π cm3 và bề dày không đáng kể. Tính bán kính đáy R, đơn vị cm của lọ để tốn ít nguyên liệu sản xuất lọ nhất (kể cả nắp lọ).
Trả lời:
Một em nhỏ cân nặng 20 kg trượt trên cầu trượt dài 3 m. Biết rằng cầu trượt có góc nghiêng so với phương nằm ngang là 30∘. Cho biết công A sinh bởi một lực F có độ dịch chuyển d được tính bởi công thức A=F.d. Tính công sinh bởi trọng lực P khi em nhỏ trượt hết chiều dài cầu trượt biết gia tốc rơi tự do g=9,8 m/s2.

Trả lời:
Cho bảng mẫu số liệu ghép nhóm sau:
| Nhóm | Tần số |
| [20;26) | 7 |
| [26;32) | 9 |
| [32;38) | 5 |
| [38;44) | 4 |
| [44;50) | 11 |
Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên. (Làm tròn kết quả đến chữ số hàng phần trăm)
Trả lời:
