Bài học cùng chủ đề
- Một số hệ thức về cạnh và đường cao trong tam giác vuông (Phần 1)
- Một số hệ thức về cạnh và đường cao trong tam giác vuông (Phần 2)
- Bài tập: Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Phiếu bài tập
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Một số hệ thức về cạnh và đường cao trong tam giác vuông SVIP
| Cho tam giác ABC vuông tại A, cạnh huyền BC = a, các cạnh góc vuông AB = c và AC = b. Gọi AH = h là đường cao ứng với cạnh huyền và CH = b', BH = c' lần lượt là hình chiếu của AC và AB trên cạnh huyền BC. |
1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
Định lý 1
Trong tam giác ABC vuông tại A (h.1), ta có:
$b^2=ab'$;$c^2=ac'$. (1)
2. Một số hệ thức liên quan tới đường cao
Định lý 2
Định lí 2 thiết lập mối quan hệ giữa đường cao ứng với cạnh huyền và các hình chiếu của hai cạnh góc vuông trên cạnh huyền của một tam giác vuông. Định lí 3 dưới đây thiết lập mối quan hệ giữa đường cao này với cạnh huyền và hai cạnh góc vuông.
Định lý 3
Từ công thức tính diện tích tam giác, ta nhanh chóng suy ra hệ thức 3.
Ta có, diện tích tam giác $ABC$ bằng: $\dfrac{1}{2}AH.BC$
Mặt khác, tam giác $ABC$ vuông tại $A$ nên diện tích có thể được tính bằng: $\dfrac{1}{2}AB.AC$
Suy ra: $\dfrac{1}{2}AH.BC=\dfrac{1}{2}AB.AC$
Do đó, $AH.BC=AB.AC$.
Định lý 4
Ta thấy, kết quả 2 bài tập đều hoàn toàn giống nhau. Từ kết quả trên ta có định lý sau:
TỔNG KẾT BÀI HỌC
| Cho tam giác $ABC$ vuông tại $A$. Đường cao $AH$ ứng với cạnh huyền $BC$. |
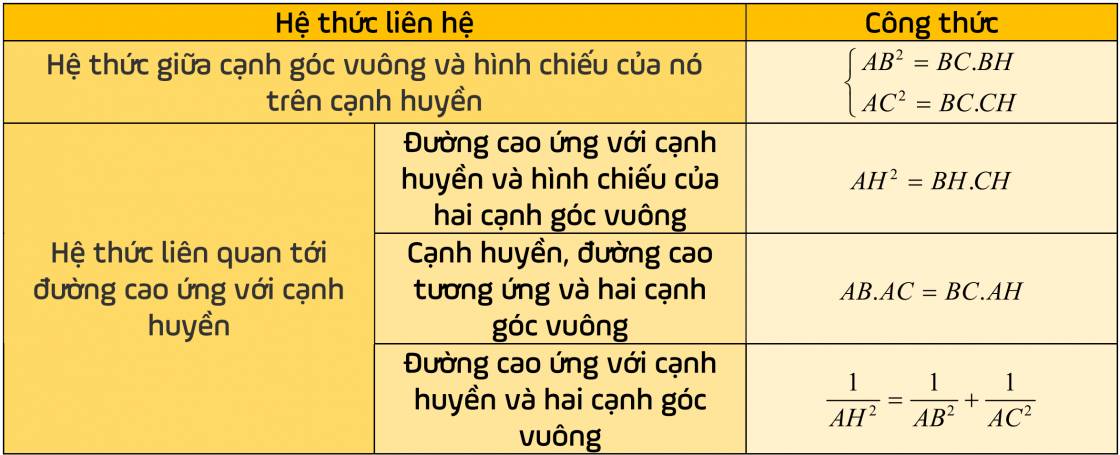
Bảng tổng hợp công thức liên hệ giữa cạnh và đường cao trong tam giác vuông
Bạn có thể đăng câu hỏi về bài học này ở đây
