Đề ôn tập và kiểm tra giữa học kì I toán 10 mới nhất

Câu 1 (1đ):

Phủ định của mệnh đề: " $3$ là số tự nhiên" là

3

là số hữu tỉ.

3

là số nguyên.

3

là số vô tỉ.

3

không phải là số tự nhiên.

Câu 2 (1đ):

Cho mệnh đề chứa biến $P(x)$ : " $x^2-5x+4=0$ ". Mệnh đề nào sau đây đúng?

P(5 )

.

P(1 )

.

P(7 )

.

P(6 )

.

Câu 3 (1đ):

Tập hợp nào sau đây là cách viết khác của tập hợp $C=\Big\{ x \in \mathbb{R} \, \big| \, 2 < x \le 5 \Big\}$ ?

C=\left[ 2\,;\,5 \right]

.

C=\left( 2\,;\,5 \right]

.

C=\left[ 2\,;\,5 \right)

.

C=\left( 2\,;\,5 \right)

.

Câu 4 (1đ):

Hệ nào sau đây không phải là hệ bất phương trình bậc nhất hai ẩn?

\left\{ \begin{aligned}&2y>0 \\&x+y\lt 1 \\\end{aligned} \right.

.

\left\{ \begin{aligned}&x-2y>0 \\&x+y\lt 1 \\\end{aligned} \right.

.

\left\{ \begin{aligned}&x>0 \\&y\lt 1 \\\end{aligned} \right.

.

\left\{ \begin{aligned}&x^2-2y>0 \\&x+y\lt 1 \\\end{aligned} \right.

.

Câu 5 (1đ):

Cặp số $(1 ; 3)$ là nghiệm của bất phương trình nào sau đây?

x-y\lt 0

.

x-y+7\lt 0

.

2x-3y-1>0

.

4x>3y

.

Câu 6 (1đ):

Khẳng định nào sau đây đúng?

\tan 30^{\circ }=\tan 150^{\circ }

.

\tan 30^{\circ }=\cot 150^{\circ }

.

\sin 120^{\circ }=\sin 60^{\circ }

.

\sin 120^{\circ }=\cos 60^{\circ }

.

Câu 7 (1đ):

Trong tam giác $ABC$ có $\widehat{B}=120^\circ$ thì đẳng thức nào sau đây đúng?

AC^2=BC^2+AB^2-3BC.AB

.

AC^2=BC^2+AB^2+BC.AB

.

AC^2=BC^2+AB^2+3BC.AB

.

AC^2=BC^2+AB^2-BC.AB

.

Câu 8 (1đ):

Mệnh đề phủ định của "Hà Nội là thủ đô của nước Việt Nam" là

"Hà Nội là thành phố thuộc miền nam Việt Nam".

"Hà Nội là thành phố có diện tích lớn nhất Việt Nam".

"Hà Nội không phải là thủ đô của nước Việt Nam".

"Hà Nội là thành phố đông dân nhất Việt Nam".

Câu 9 (1đ):

Cho ba tập hợp $A=\left(-\infty ;0 \right]$ , $B=\left(1;+\infty \right)$ và $C=\left[ 0;1 \right)$ . Khi đó $\left(A\cup B \right) \cap C$ bằng

\varnothing

.

\mathbb{R}

.

\left\{ 0;1 \right\}

.

\left\{ 0 \right\}

.

Câu 10 (1đ):

Cho tập hợp $A=\left\{ 1;2;3;4;5 \right\}$ . Số tập hợp $X$ thỏa mãn $A \backslash X=\left\{ 1;3;5 \right\}$ và $X\backslash A=\left\{ 6;7 \right\}$ là

1

.

2

.

3

.

4

.

Câu 11 (1đ):

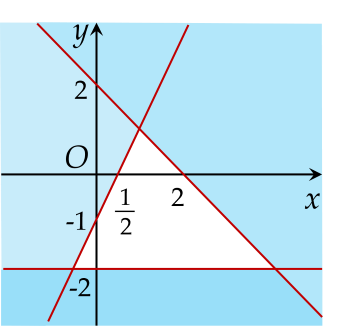
Phần không tô màu trong hình vẽ biểu diễn miền nghiệm của hệ bất phương trình nào dưới đây?

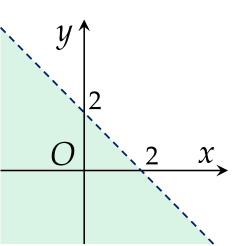
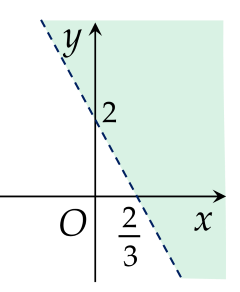
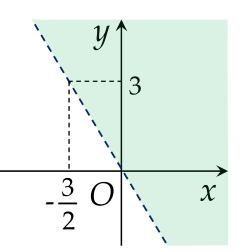
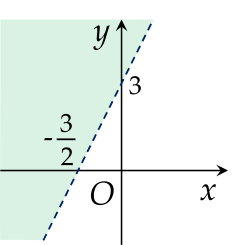
loading...

\left\{ \begin{aligned} & 2x-y<1 \\ & x+y<2 \\ & 3y-x>0 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & 2x-y<1 \\ & x+y\ge 2 \\ & y\ge -2 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & 2x-y\ge 1 \\ & x+y\le 2 \\ & y\ge -2 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & 2x-y\ge 1 \\ & 2x+y>2 \\ & 3y-x>0 \\ \end{aligned} \right.

.

Câu 12 (1đ):

Phần tô màu (không bao gồm đường thẳng nét đứt) trong hình nào sau đây là miền nghiệm của bất phương trình $2x-y+3<0$ ?

Câu 13 (1đ):

Lớp 10A có tất cả $40$ học sinh trong đó có $13$ học sinh chỉ thích đá bóng, $18$ học sinh chỉ thích chơi cầu lông và số học sinh còn lại thích chơi cả hai môn thể thao nói trên.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Có $9$ học sinh thích chơi cả hai môn cầu lông và bóng đá.
b) Có $22$ học sinh thích bóng đá.
c) Có $26$ học sinh thích cầu lông.
d) Có $21$ học sinh chỉ thích chơi một trong hai môn cầu lông và bóng đá.

Câu 14 (1đ):

Đô thích ăn hai loại trái cây là cam và xoài, mỗi tuần mẹ cho Đô $200$ nghìn đồng để mua trái cây. Biết rằng giá cam là $15$ $000$ đồng/ $1$ kg, giá xoài là $30$ $000$ đồng/ $1$ kg. Gọi $x, \, y$ (với $a > 0; \, y > 0$ ) lần lượt là số ki-lô-gam cam và xoài mà Đô có thể mua về sử dụng trong một tuần.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Trong tuần, số tiền Đô có thể mua cam là $15 \, 000x$ đồng, số tiền An có thể mua xoài là $30 \, 000y$ đồng.
b) $3x+6y \ge 40$ .
c) Đô không thể mua đủ $5$ kg cam, $4$ kg xoài sử dụng trong tuần.
d) Đô có thể mua $4$ kg cam, $6$ kg xoài sử dụng trong tuần.

Câu 15 (1đ):

Cho góc $\alpha$ thoả mãn $\sin \alpha =\dfrac{3}{5}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\sin^2 \alpha =\dfrac{9}{25}$ .
b) $\cos^2 \alpha =\dfrac{16}{25}$ .
c) $\dfrac{\cot \alpha +\tan \alpha }{\cot \alpha -\tan \alpha }=\dfrac{25}{7}$ .
d) $\dfrac{1}{\cos^2 \alpha - \sin^2 \alpha}=\dfrac{7}{25}$ .

Câu 16 (1đ):

Lớp 10A trường THPT Kon Tum có $39$ bạn học sinh. Do trường có tổ chức Hội Thao cấp trường cho học sinh với hai môn là bóng bàn và cầu lông nên lớp đã chọn ra các bạn học sinh để đi dự thi. Biết rằng có $21$ bạn chơi bóng bàn, $15$ bạn chơi cầu lông và $7$ bạn chơi cả bóng bàn và cầu lông.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Có $9$ bạn vừa chơi bóng bàn vừa chơi cầu lông.
b) Có $36$ bạn chơi bóng bàn hoặc cầu lông.
c) Có $10$ bạn không chơi cả hai môn.
d) Số bạn chỉ chơi đúng $1$ môn bóng bàn hoặc cầu lông là $17$ bạn.

Câu 17 (1đ):

Cho tập hợp $A=\left\{ 1;2 \right\}$ và tập hợp $B=\big\{ x\in \mathbb{R} \, \big| \, x^2 + (m+2)x-2m-8=0 \big\}$ . Có bao nhiêu giá trị nguyên của tham số $m$ sao cho $B\subset A$ ?

Trả lời:

Câu 18 (1đ):

Lớp có $45$ học sinh trong đó có $25$ em học sinh học giỏi môn Toán, $23$ em học sinh học giỏi môn Văn, $20$ em học sinh học giỏi môn Tiếng Anh. Đồng thời có $11$ em học sinh học giỏi cả môn Toán và môn Văn, $8$ em học sinh học sinh giỏi cả môn Văn và môn Tiếng Anh, $9$ em học sinh học giỏi cả môn Toán và môn Tiếng Anh, biết rằng mỗi học sinh trong lớp học giỏi ít nhất một trong ba môn Toán, Văn, Tiếng Anh. Lớp 10A có bao nhiêu bạn học giỏi cả ba môn Toán, Văn, Tiếng Anh?

Trả lời:

Câu 19 (1đ):

Tìm các nghiệm $(x;y)$ của bất phương trình $\dfrac{x}{2}+\dfrac{y}{3}-1\le 0$ . Trong đó $x,y$ là các số nguyên dương. Tính $x + y$ .

Trả lời:

Câu 20 (1đ):

Một xưởng sản xuất hai loại sản phẩm là sản phẩm loại I và sản phẩm loại II:

▪️ Mỗi kg sản phẩm loại I cần $2$ kg nguyên liệu và $30$ giờ, thu lời (lãi) được $40$ nghìn đồng.

▪️ Mỗi kg sản phẩm loại II cần $4$ kg nguyên liệu và $15$ giờ, thu lời được $30$ nghìn đồng.

Xưởng có $200$ kg nguyên liệu và $1 \, 200$ giờ làm việc tối đa. Để có mức tiền lãi cao nhất, xưởng cần sản xuất $a$ sản phẩm loại I và $b$ sản phẩm loại II. Tính $a + b$ .

Trả lời:

Câu 21 (1đ):

Gọi $a$ , $b$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $L=y-x$ , với $x$ và $y$ thỏa mãn hệ bất phương trình $\left\{ \begin{aligned} & 2x+3y-6 \le 0 \\ & 2x-3y-1 \le 0 \\ & x \ge 0 \\ \end{aligned} \right.$ . Tính $11a+12b$ .

Trả lời:

Câu 22 (1đ):

Người $A$ đứng ở đỉnh của tòa nhà và quan sát chiều diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của người A tới chiếc diều và phương nằm ngan) là $\alpha =35^{\circ }$ ; khoảng cách từ đỉnh tòa nhà tới mắt người $A$ là $1,5$ m. Cùng lúc đó ở dưới chân tòa nhà, người $B$ cũng quan sát chiếc diều và thấy góc nâng là $\beta =75^{\circ }$ ; khoảng cách từ mặt đất đến mắt người $B$ cũng là $1,5$ m. Biết chiều cao của tòa nhà là $h=20$ m.

Chiếc diều bay cao bao nhiêu mét so với mặt đất (làm tròn kết quả đến hàng đơn vị)?

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 7) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 7) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Cảnh báo

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP