Bài học cùng chủ đề
Góc và cạnh của một tam giác SVIP
1. TỔNG BA GÓC TRONG TAM GIÁC
Tổng ba góc trong một tam giác bằng $180^{\circ}$.
Ví dụ 1. Tìm số đo các góc chưa biết của các tam giác trong hình vẽ dưới đây.
Lời giải
Áp dụng định lí về tổng số đo ba góc của tam giác, ta có:
a) \(\widehat{C}=180^\circ-32^\circ-58^\circ=90^\circ\).
b) \(\widehat{F}=180^\circ-68^\circ-42^\circ=70^\circ\).
c) \(\widehat{I}=180^\circ-27^\circ-56^\circ=97^\circ\).
Chú ý:
⚡Tam giác $FGH$ có ba góc đều nhọn nên gọi là tam giác nhọn.
⚡Tam giác $IJK$ có một góc tù nên gọi là tam giác tù.
⚡Tam giác $CDE$ có một góc vuông nên gọi là tam giác vuông. Trong tam giác $CDE$ vuông tại $C$, $CD$ và $CE$ là hai cạnh góc vuông, $DE$ là cạnh huyền.
Tam giác $CDE$ có: \(\widehat{D}+\widehat{E}=58^\circ+32^\circ=90^\circ\).
Nhận xét: Hai góc có tổng bằng $90^{\circ}$ được gọi là hai góc phụ nhau. Trong tam giác vuông, hai góc nhọn phụ nhau.
Câu hỏi:
@200428092111@
GÓC NGOÀI CỦA TAM GIÁC
Cho tam giác $MNP$ tại đỉnh $P$ vẽ tia $Px$ là tia đối của tia $PN$.
Góc $MPx$ được gọi là góc ngoài tại $P$ của tam giác $MNP$.
Góc $MPx$ không kề với hai góc $M$ và $N$ của tam giác $MNP$.
Mỗi góc ngoài của một tam giác có số đo bằng tổng số đo hai góc trong không kề với nó.
Ví dụ 2. Cho tam giác $ABC$ có $\widehat{A}=30^\circ$, $\widehat{B}=70^\circ$. $\widehat{BCD}$ là góc ngoài tại đỉnh $C$ của tam giác $ABC$. Tính số đo $\widehat{ACD}$.
Lời giải
Theo tính chất góc ngoài của tam giác, ta có:
$\widehat{BCD}=\widehat{A}+\widehat{B}=30^\circ+70^\circ=100^\circ$.
Câu hỏi:
@200428091405@@205079283531@@205079409803@
2. QUAN HỆ GIỮA BA CẠNH CỦA MỘT TAM GIÁC
Trong một tam giác, độ dài của một cạnh bất kì luôn nhỏ hơn tổng độ dài hai cạnh còn lại.
Ví dụ 3. Cho tam giác $ABC$ khi đó
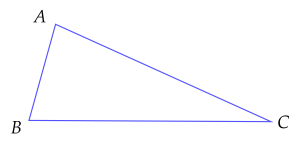
⚡ $AB<AC+BC$
⚡ $AC<AB+BC$
⚡ $BC<AB+AC$
Trong một tam giác, độ dài của một cạnh bất kì luôn lớn hơn hiệu độ dài hai cạnh còn lại.
Ví dụ 4. Cho tam giác $ABC$ khi đó
⚡ $AB>AC-BC$
⚡ $AC>BC-AB$
⚡ $BC>AC-AB$
Chú ý:
⚡ Nếu ba độ dài $a$, $b$, $c$ không thỏa mãn một bất đẳng thức tam giác thì chúng không phải là độ dài ba cạnh của một tam giác.
⚡ Để kiểm tra $a$, $b$, $c$ có là độ dài ba cạnh của một tam giác hay không, ta chỉ cần so sánh độ dài lớn nhất có nhỏ hơn tổng hai độ dài còn lại hoặc độ dài nhỏ nhất có lớn hơn hiệu hai độ dài còn lại hay không.
Ví dụ 5. Hãy kiểm tra ba độ dài sau đây có thể là độ dài ba cạnh của một tam giác.
a) $3$ cm, $5$ cm, $9$ cm.
b) $4$ cm, $5$ cm, $8$ cm.
Lời giải
a) Ta có $3+5=8<9$ do đó ba độ dài $3$ cm, $5$ cm, $9$ cm không thỏa mãn một bất đẳng thức tam giác nên không là độ dài ba cạnh của một tam giác.
b) Ta có $4>8-5=3$, ba độ dài $4$ cm, $5$ cm, $8$ cm thỏa mãn điều kiện trong chú ý nên là độ dài ba cạnh của một tam giác.
Câu hỏi:
@204549745417@
Ví dụ 6. Người ta đặt một trạm phát sóng 4G tại vị trí $A$. Có một đảo nhỏ (tại vị trí $B$) chưa biết khoảng cách đến vị trí $A$ nhưng lại biết khoảng cách từ đảo đó đến một khách sạn (tại vị trí $C$) là $75$ km và khách sạn đó cách vị trí $A$ là $20$ km. Sóng 4G của trạm phát sóng tại vị trí $A$ có thể phủ đến đảo đó được không? Vì sao?
Biết rằng sóng 4G có thể phủ đến bán kính $100$ km.
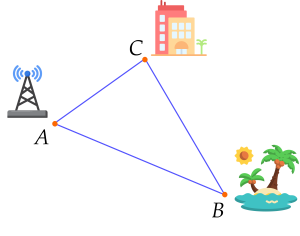
Lời giải
Ba vị trí $A$, $B$, $C$ tạo thành ba đỉnh của tam giác $ABC$.
Khi đó $AB < AC + BC$ (bất đẳng thức tam giác).
Suy ra $AB < 20 + 75 = 95 < 100$.
Do đó sóng 4G của trạm phát sóng tại vị trí $A$ có thể phủ đến đảo $B$.
Câu hỏi:
@204549783220@@204549786495@