a)

MAB

Vì điểm $M$ là trung điểm của đoạn thẳng $AB$.

Suy ra $AM=MB=\dfrac{AB}2=\dfrac 42=2 (cm).

b) 

 Trường hợp 1.

MABxy

xMy^=60∘xMy​=60∘.

 Trường hợp 2.

MABxy

xMy^=160∘xMy​=160∘.

1)

a) Tập hợp các điểm thuộc đoạn thẳng $BD$ là $B;C;D$, tập hợp các điểm thuộc không đoạn thẳng $BD$ là $A;E$.

b) Cặp đường thẳng song song là $AB$ // $DE$.

c) Gợi ý: Liệt kê theo các giao điểm, có 5 giao điểm nên có 5 cặp đường thẳng cắt nhau.

Các cặp đường thẳng cắt nhau là

$AB$ và $AE$ cắt nhau tại $A$.

$BA$ và $BD$ cắt nhau tại $B$.

$AE$ và $BD$ cắt nhau tại $C$.

$DE$ và $DB$ cắt nhau tại $D$.

$EA$ và $ED$ cắt nhau tại $E$.

2) 

a) 

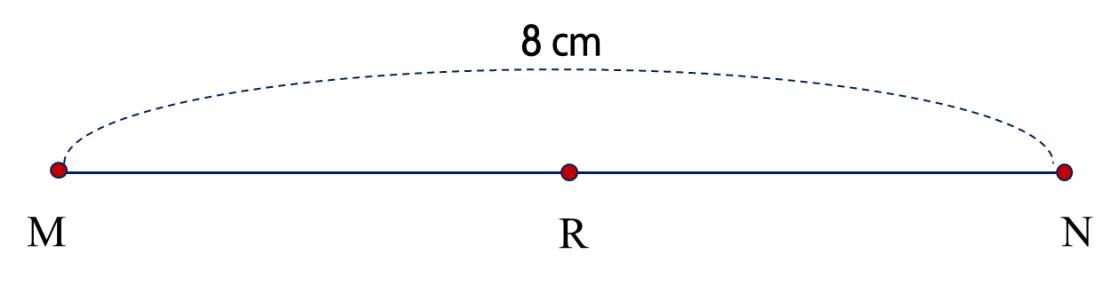
Vì $R$ là trung điểm của đoạn thẳng $MN$, nên ta có $MR=RN=MN:2$.

Độ dài của đoạn thẳng $MR$ hay $RN$ là:

$8:2=4$ (cm)

b)

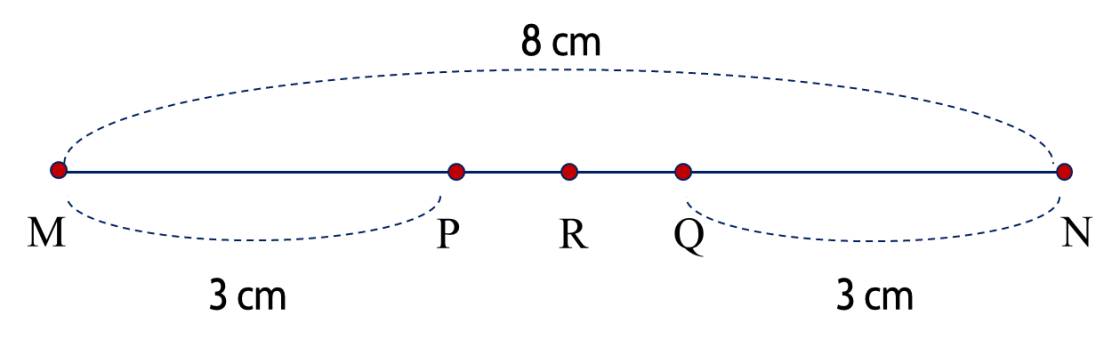
Nhìn hình vẽ, ta thấy $R$ nằm giữa $P$ và $Q$; $MN=MP+PQ+QN$; $MR=MP+PR$.

Độ dài của đoạn thẳng $PQ$ là

$8-3-3=2$ (cm).

Độ dài của đoạn thẳng $PR$ là

$4-3=1$ (cm).

Từ đây, ta thấy PR:PQ=12PR:PQ=21​,

Vậy $R$ là trung điểm $PQ$.

3)

Chọn 1 điểm nối với $11$ điểm còn lại ta được $11$ đường thẳng, làm như thế với $12$ điểm ta được $12.(12-1)=132$ đường thẳng. Nhưng mỗi đường thẳng lặp lại $2$ lần nên số đường thẳng vẽ được là $132:2=66$ đường thẳng.

Qua $4$ điểm không thẳng hàng sẽ vẽ được $6$ đường thẳng.

Qua $4$ điểm thẳng hàng vẽ được $1$ đường thẳng nên số đường thẳng giảm đi $5$ đường thẳng

Vậy số đường thẳng vẽ được là $66-5=61$ đường thẳng vậy ta vẽ được 61 đường thẳng.

a) Có $3$ kết quả khác nhau trong mỗi lần lấy bóng là:

- Hòa lấy ra quả bóng đỏ (kí hiệu: Đ).

- Hòa lấy ra quả bóng xanh (kí hiệu: X).

- Hòa lấy ra quả bóng vàng (kí hiệu: V).

b) Hai điều chú ý của mô hình xác suất là:

- Hòa lấy ra ngẫu nhiên một quả bóng trong hộp.

- Tập hợp các kết quả có thể xảy ra là: {Đ, X, V}. Các kí hiệu được giải thích ở phần trên.

c) Trong $9$ lần lấy ngẫu nhiên, có $4$ lần bạn Hòa lấy ra quả bóng màu Xanh.

Xác suất thực nghiệm của kết quả bạn Hòa lấy ra quả bóng màu Xanh là:

4:9=494:9=94​
 

Ta có $xy=-3=(-1).3=1.(-3)$.

Do đó:

+) $x=-1$; $y=3$ suy ra $x+y=(-1)+3=2$ (nhận);

+) $x=3$; $y=-1$ suy ra $x+y=3+(-1)=2$ (nhận);

+) $x=-3$; $y=1$ suy ra $x+y=(-3)+1=-2$ (loại);

+) $x=1$; $y=-3$ suy ra $x+y=1+(-3)=-2$ (loại).

Vậy ta có các cặp số ($x$; $y$) là $(-1;3)$ và $(3;-1)$.

Diện tích ao mới gấp bốn lần diện tích của ao cũ nên diện tích tăng thêm gấp $3$ lần diện tích ao cũ.

Diện tích ao cũ là:

     $600:$ $3=200$ (m${}^2$)

Diện tích ao mới là:

     $200.4=800$ (m${}^2$)

Vì ao mới có chiều dài gấp hai lần chiều rộng nên ta chia ao mới thành hai hình vuông có diện tích bằng nhau.

Diện tích một hình vuông là:

     $800:2=400$ (m${}^2$)

Suy ra chiều rộng ao mới là $20$ m.

Chiều dài ao mới là:

     $20.2=40$ (m)

Chu vi ao mới là:

     $\left(40+20\right).2=120$ (m)

Số cọc để rào xung quanh ao mới là:

     $\left(120-2\right):1+1=118+1=119$ (cọc).

a) Vì $x$ $⋮$ $3$; $x$ $⋮$ $5$; $x$ $⋮$ $7$ và $x$ nhỏ nhất nên $x$ = BCNN($3$ , $5$,  $7$).

Mà BCNN($3$ , $5$,  $7$) = $\mathrm{3.5.7}=105$.

Vậy $x=105$.

b) Gọi số phần quà nhiều nhất có thể chia là $x$ (phần quà), $x\in {\mathbb{N}}^{\ast }$.

Theo bài ra ta có $24⋮x$; $36⋮x$; $60⋮x$; $x$ là nhiều nhất.

Suy ra $x=$ ƯCLN$(24,36,60)$.

$24=2^3.3$; $36=2^2.3^2$; $60=2^2.3.5$.

Suy ra $x=12$.

Vậy mỗi túi có $2$ gói bánh, $3$ hộp sữa, $5$ khăn len.

a) $53.25-25.12+75.53$

$=\left(53.25+75.53\right)-25.12$

$=53.\left(25+75\right)-25.12$

$=53.100-300$

$=5300-300$

$=5000$.

b) $260:\left[5+7.\left(72:2^3-6\right)\right]-3^2$

$=260:\left[5+7.\left(72:8-6\right)\right]-9$

$=260:\left[5+7.3\right]-9$

$=260:26-9$

$=10-9$

$=1$.