Câu 1.

Văn bản được viết theo thể thơ lục bát.

Câu 2.

Hai dòng thơ trên là lời đối thoại trực tiếp của nhân vật.

Câu 3.

Tác giả sử dụng nhiều từ láy như: sè sè, dầu dầu, vắng tanh, lạnh ngắt, lờ mờ, dầm dầm…
→ Các từ láy giúp:

• Gợi cảnh hoang vắng, buồn bã.
• Thể hiện cảm xúc xót xa của nhân vật.
• Làm cho bài thơ giàu hình ảnh và cảm xúc.

Câu 4.

Trước số phận của Đạm Tiên, Thúy Kiều thương xót, đau buồn và đồng cảm sâu sắc.
→ Điều đó cho thấy Thúy Kiều là người nhân hậu, giàu tình cảm, biết thương người.

Câu 5.

Bài học rút ra:
→ Cần biết yêu thương, cảm thông với những người có số phận bất hạnh.

Vì:
Sự quan tâm và lòng nhân ái giúp cuộc sống trở nên tốt đẹp và ý nghĩa hơn.

Tam giác ABD nội tiếp trong đường tròn (O) có AB là đường kính nên 

Tam giác AEC nội tiếp trong đường tròn (O’) có AC là đường kính nên 

Mặt khác: 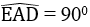 (chứng minh trên)

Tứ giác ADME có ba góc vuông nên nó là hình chữ nhật.

∆BCD có OO' là đường trung bình suy ra OO' ∕∕ CD.

∆ABC có OI là đường trung bình suy ra OO' ∕∕ CA.

Do đó A, C, D thẳng hàng.

Ta có: ∆BOO' vuông tại B suy ra ∆BCD vuông tại B.

Do đó diện tích tam giác BCD là: S = 12BC.BD=12.6.8=24 cm².

a) Ta có: OA+O'A>OO'(12+5>13)⇒(O) và (O’) cắt nhau tại 2 điểm phân biệt

b) Ta có: OA2+O'A2=52+122=169=132=OO'2⇒ΔOAO' vuông tại A (định lý Pytago đảo)⇒OA⊥O'A

Vì A∈(O')⇒OA là tiếp tuyến của (O’)

Gọi M=AB∩OO'

Theo tính chất 2 đường tròn cắt nhau ⇒AB là đường trung trực OO'⇒M là trung điểm OO'.ΔOAO' vuông tại A, có AM đường cao

⇒1AM2=1AO2+1AO'2 (hệ thức lượng) hay 1AM2=1122+152⇒AM=6013(cm)

⇒AB=2AM=2.6013=12013(cm)

b) Ta có:

• \(A\) nằm trên đường tròn tâm \(O\), bán kính \(2 \textrm{ } \text{cm}\) nên \(O A = 2 \textrm{ } \text{cm}\).
• Hai đường tròn \(\left(\right. O ; 2 \left.\right)\) và \(\left(\right. A ; 2 \left.\right)\) cắt nhau tại \(C\).

⇒ \(O C = 2 \textrm{ } \text{cm}\) và \(A C = 2 \textrm{ } \text{cm}\).

→ \(O\) và \(A\) cách \(C\) đều \(2 \textrm{ } \text{cm}\).

a) Qua \(O\) kẻ đường thẳng đi qua \(M\), lấy điểm \(N\) sao cho \(O\) là trung điểm của \(M N\).

b) Từ \(M\) hạ vuông góc xuống \(A B\) tại \(H\), lấy điểm \(P\) đối diện \(M\) qua \(A B\) sao cho \(H\) là trung điểm của \(M P\).

a) Vì \(A B = 4 \textrm{ } \text{cm}\) không đổi nên
→ \(A\) di động trên đường tròn tâm \(B\), bán kính \(4 \textrm{ } \text{cm}\).

b) Gọi \(M\) là trung điểm của \(A C\).
Khi \(A\) di chuyển trên đường tròn tâm \(B\), bán kính \(4 \textrm{ } \text{cm}\),
→ \(M\) di chuyển trên đường tròn tâm \(B^{'}\) (với \(C B^{'} = \frac{1}{2} C B\)), bán kính \(2 \textrm{ } \text{cm}\).

a) Qua \(O\) kẻ đường thẳng đi qua \(M\), lấy điểm \(N\) sao cho \(O\) là trung điểm của \(M N\).

b) Từ \(M\) hạ vuông góc xuống \(A B\) tại \(H\), lấy điểm \(P\) đối diện \(M\) qua \(A B\) sao cho \(H\) là trung điểm của \(M P\).

a) Ta có: OA′OA=rR;OB′OB=rR,  suy ra OA′OA=OB′OB.

b) Xét ∆OAB có OA′OA=OB′OB  nên AB // A’B’ (theo định lí Thales đảo).