Giới thiệu về bản thân



































Ta có: ˆACB=90o (góc nội tiếp chắn nửa đường tròn)
Xét △AOC có AO=OC=AC=R
→△AOC là tam giác đều.
→ˆA=60o
Áp dụng định lý tổng ba góc của tam giác:
ˆB=180o−ˆACB−ˆB
=180o−90o−60o=30o
Vậy ˆA=60o, ˆB=30o, ˆACB=90o

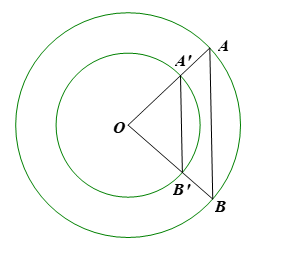
a) Ta có: OA′OA=rR;OB′OB=rR, suy ra OA′OA=OB′OB.
b) Xét ∆OAB có OA′OA=OB′OB nên AB // A’B’ (theo định lí Thalès đảo).
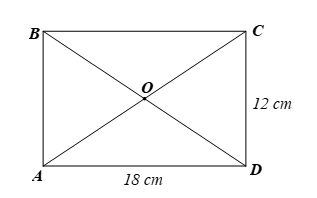
⦁ Vì ABCD là hình chữ nhật nên AC = BD. (1)
Gọi O là giao điểm của hai đường chéo AC, BD của hình chữ nhật.
Khi đó, O là trung điểm của AC và BD (tính chất hình chữ nhật) nên OA=OC=12AC;OB=OD=12BD. (2)
Từ (1) và (2) ta có OA=OC=OB=OD=12AC=12BD.
Vậy bốn điểm A, B, C, D cùng thuộc một đường tròn đường kính AC, BD.
⦁ Vì ABCD là hình chữ nhật nên ˆADC=90°.
Xét ∆ADC vuông tại D, theo định lí Pythagore, ta có:
AC2 = AD2 + DC2 = 182 + 122 = 468.
Do đó AC=√468=√62⋅13=6√13 (cm).
Vậy bán kính đường tròn đi qua bốn điểm A, B, C, D là 12AC=12⋅6√13=3√13 (cm).
a) Vì hai đường tròn (A; 6 cm) và (B; 4 cm) cắt nhau tại C và D nên C, D cùng nằm trên hai đường tròn (A; 6 cm) và (B; 4 cm), do đó AC = AD = 6 cm và BC = BD = 4 cm.
b) Do I là giao điểm của đường tròn (B; 4 cm) với đoạn thẳng AB nên I nằm giữa hai điểm A, B và I nằm trên đường tròn (B; 4 cm), do đó BI = 4 cm.
Vì I nằm giữa hai điểm A, B nên ta có: AI + IB = AB
Suy ra AI = AB – IB = 8 – 4 = 4 (cm).
Ta có I nằm giữa hai điểm A, B và AI = BI nên I là trung điểm của đoạn thẳng AB.
c) Do K là giao điểm của đường tròn (A; 6 cm) với đoạn thẳng AB nên K nằm trên đường tròn (A; 6 cm), do đó AK = 6 cm.
Ta có AI < AK (4 cm < 6 cm) nên I nằm giữa hai điểm A, K.
Do đó AI + IK = AK
Suy ra IK = AK – AI = 6 – 4 = 2 (cm).
Vậy IK = 2 cm.
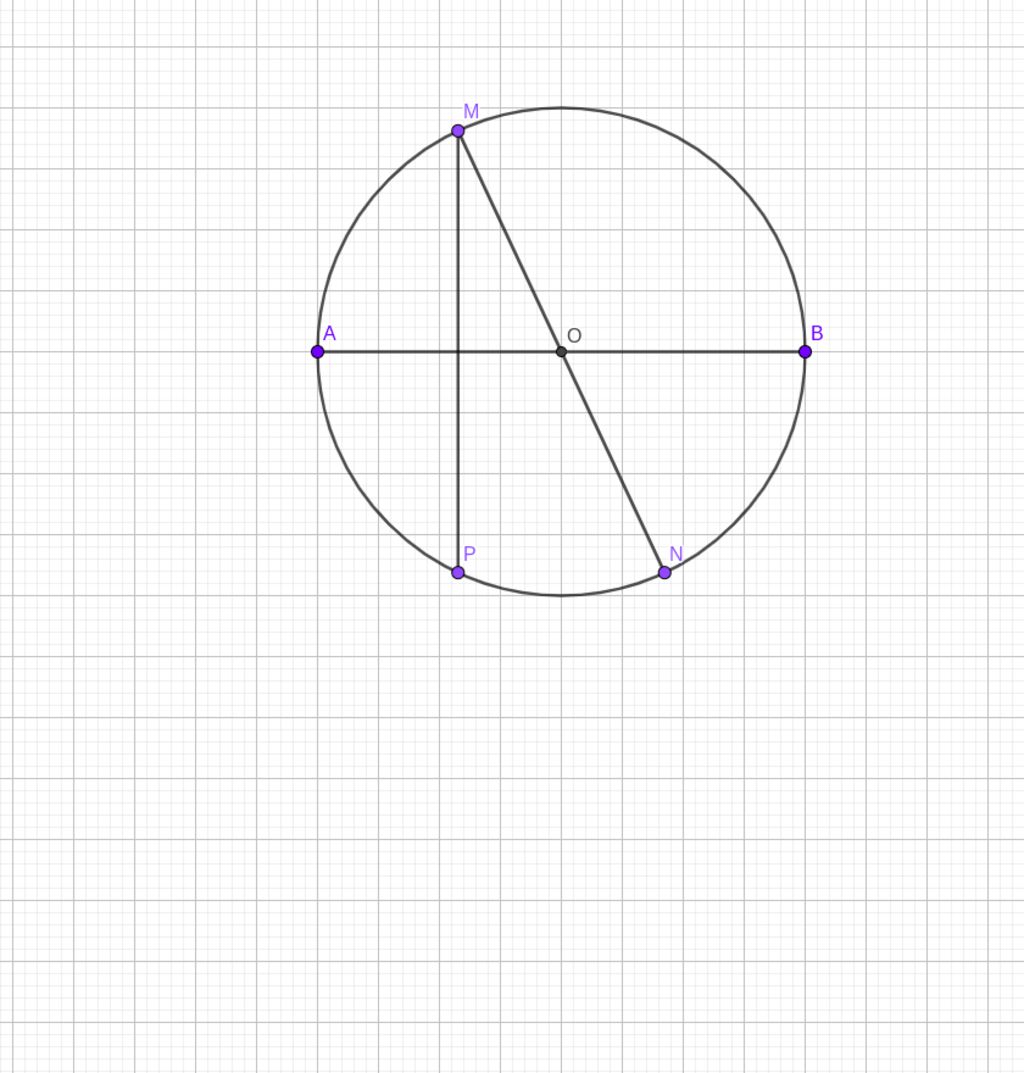
a.Gọi MO∩(O)=N,M≠N
→M,N đối xứng qua O
→N đối xứng với M qua O
b.Kẻ MP⊥AB=P,P∈(O),P≠M
→P đối xứng với N qua AB
a/
BC cố định => B cố định
AB=4 cm không đổi
=> A chạy trên đường tròn tâm B bán kính AB
b/
Từ M dựng đường thẳng // AB cắt BC tại D
=> D là trung điểm của BC (Trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với cạnh thứ 2 thì đi qua trung điểm cạnh còn lại)
=> MD là đường trung bình của tg ABC => \(M D = \frac{A B}{2}\)
Ta có BC cố định =>D cố định
MD không đổi
=> M chạy trên đường tròn tâm D bán kính MD
a/
BC cố định => B cố định
AB=4 cm không đổi
=> A chạy trên đường tròn tâm B bán kính AB
b/
Từ M dựng đường thẳng // AB cắt BC tại D
=> D là trung điểm của BC (Trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với cạnh thứ 2 thì đi qua trung điểm cạnh còn lại)
=> MD là đường trung bình của tg ABC => \(M D = \frac{A B}{2}\)
Ta có BC cố định =>D cố định
MD không đổi
=> M chạy trên đường tròn tâm D bán kính MD
a) Mở một chiếc compa sao cho hai đầu compa cách nhau một khoảng bằng 2 cm. Đặt đầu nhọn của compa lên điểm C, xoay compa để đầu bút của compa vạch trên giấy một đường tròn, ta được đường tròn (C; 2 cm).
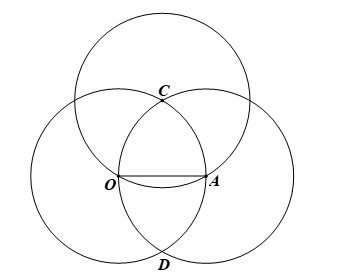
b) Vì C là giao điểm của hai đường tròn (O; 2 cm) và (A; 2 cm) nên C nằm trên cả hai đường tròn, do đó OC = 2 cm và CA = 2 cm.
Suy ra hai điểm O, A cùng nằm trên đường tròn (C; 2 cm).
Vậy đường tròn (C; 2 cm) đi qua hai điểm O và A.