Giới thiệu về bản thân



































Xét tam giác \(A B C\), áo dụng tính chất tia phân giác trong tam giác, ta có:
\(\frac{A M}{M B} = \frac{A C}{C B} = \frac{A B}{C B} = \frac{A N}{N C} \left(\right. = \frac{b}{a} \left.\right)\)
Vậy \(M N\) // \(B C\) (Định lí đảo của định lí Thalès)
Suy ra \(\frac{M N}{B C} = \frac{A M}{A B} = \frac{b}{b + a}\) (Định lí Thalès)
Vậy nên \(M N = \frac{a b}{a + b} .\)
Tam giác \(A B C\) cân tại \(A\) nên \(A B = A C = 12\) cm.
Xét tam giác \(A B C\), áp dụng tính chất tia phân giác ta có:
\(\frac{A D}{D B} = \frac{A C}{C B} = \frac{12}{6} = 2\)
Suy ra \(\frac{A D}{A B} = \frac{2}{3}\) suy ra \(A D = \frac{2}{3} . 12 = 8\) (cm)
Do đó, \(D B = 12 - 8 = 4\) (cm).
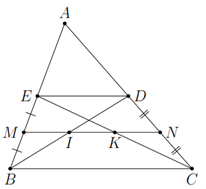
Xét \(\Delta B E D\) có \(\left{\right. & M I // E D \\ & M E = B M\) suy ra \(I D = I B\).
Xét \(\Delta C E D\) có \(\left{\right. & N K // E D \\ & N C = N D\) suy ra \(K E = K C\).
Suy ra \(M I = \frac{1}{2} E D\); \(N K = \frac{1}{2} E D\); \(E D = \frac{1}{2} B C\).
\(I K = M K - M I = \frac{1}{2} B C - \frac{1}{2} D E = D E - \frac{1}{2} D E = \frac{1}{2} D E\).
Vậy \(M I = I K = K N\).
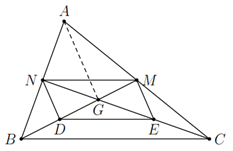
a) Vì \(B M\), \(C N\) là các đường trung tuyến của \(\Delta A B C\) nên \(M A = M C\), \(N A = N B\).
Do đó \(M N\) là đường trung bình của \(\Delta \&\text{nbsp}; A B C\), suy ra \(M N\) // \(B C\). (1)
Ta có \(D E\) là đường trung bình của \(\Delta \&\text{nbsp}; G B C\) nên \(D E\) // \(B C\). (2)
Từ (1) và (2) suy ra \(M N\) // \(D E\).
b) Xét \(\Delta \&\text{nbsp}; A B G\), ta có \(N D\) là đường trung bình.
Xét \(\Delta \&\text{nbsp}; A C G\), ta có \(M E\) là đường trung bình.
Do đó \(N D\) // \(A G\), \(M E\) // \(A G\).
Suy ra \(N D\) // \(M E\).
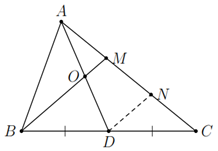
a) Qua \(D\) vẽ một đường thẳng song song với \(B M\) cắt \(A C\) tại \(N\).
Xét \(\Delta \&\text{nbsp}; M B C\) có \(D B = D C\) và \(D N\) // \(B M\) nên \(M N = N C = \frac{1}{2} M C\) (định lí đường trung bình của tam giác).
Mặt khác \(A M = \frac{1}{2} M C\), do đó \(A M = M N = \frac{1}{2} M C\).
Xét \(\Delta \&\text{nbsp}; A N D\) có \(A M = M N\) và \(B M\) // \(D N\) nên \(O A = O D\) hay \(O\) là trung điểm của \(A D\).
b) Xét \(\Delta \&\text{nbsp}; A N D\) có \(O M\) là đường trung bình nên \(O M = \frac{1}{2} D N\). (1)
Xét \(\Delta \&\text{nbsp}; M B C\) có \(D N\) là đường trung bình nên \(D N = \frac{1}{2} B M\). (2)
Từ (1) và (2) suy ra \(O M = \frac{1}{4} B M\).
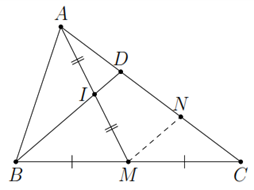
a) Kẻ \(M N\) // \(B D\), \(N \in A C\).
\(M N\) là đường trung bình trong \(\triangle C B D\)
Suy ra \(N\) là trung điểm của \(C D\) (1).
\(I N\) là đường trung bình trong \(\triangle A M N\)
Suy ra \(D\) là trung điểm của \(A N\) (2).
Từ (1) và (2) suy ra \(A D = \frac{1}{2} D C\).
b) Có \(I D = \frac{1}{2} M N\); \(M N = \frac{1}{2} B D\), nên \(B D = I D\).
Câu 1.
Bài thơ “Đề đền Sầm Nghi Đống” của Hồ Xuân Hương là tiếng cười châm biếm sắc sảo nhằm vào tên tướng giặc xâm lược đã thất bại nhục nhã trước dân tộc Việt Nam. Qua hình ảnh ngôi đền “đứng cheo leo”, nữ sĩ đã hạ thấp, chế giễu sự nghiệp và danh phận của Sầm Nghi Đống, cho thấy hắn chỉ còn là cái bóng mờ của lịch sử. Hai câu thơ cuối mang đậm chất mỉa mai, khi tác giả đặt câu hỏi về “anh hùng”, qua đó khẳng định kẻ thù xâm lược không xứng đáng với danh xưng ấy. Bài thơ không chỉ thể hiện lòng yêu nước, niềm tự hào dân tộc mà còn bộc lộ cá tính mạnh mẽ, bản lĩnh và tư tưởng tiến bộ của Hồ Xuân Hương – một người phụ nữ dám lên tiếng trước lịch sử và xã hội phong kiến.
Câu 2.
Xây dựng và bảo vệ đất nước là trách nhiệm thiêng liêng của mỗi công dân, không phân biệt tuổi tác hay nghề nghiệp. Trách nhiệm ấy không chỉ thể hiện trong những thời khắc lịch sử hào hùng mà còn được thể hiện trong từng hành động nhỏ bé của đời sống hằng ngày.
Trước hết, mỗi người cần có ý thức yêu nước đúng đắn, bắt đầu từ việc tôn trọng lịch sử, gìn giữ truyền thống văn hóa dân tộc và tự hào về cội nguồn. Trong thời bình, xây dựng đất nước thể hiện qua lao động, học tập nghiêm túc, không ngừng nâng cao tri thức, đạo đức và kỹ năng để trở thành công dân có ích. Đối với thế hệ trẻ, học tập tốt, rèn luyện nhân cách, sống có lý tưởng chính là cách thiết thực nhất để góp phần phát triển đất nước.
Bên cạnh đó, trách nhiệm bảo vệ đất nước còn thể hiện ở ý thức chấp hành pháp luật, bảo vệ môi trường, đấu tranh với các hành vi sai trái, tiêu cực trong xã hội. Trong bối cảnh hội nhập, mỗi cá nhân cần tỉnh táo trước các thông tin sai lệch, không tiếp tay cho những hành động làm tổn hại đến lợi ích quốc gia. Yêu nước không chỉ là cảm xúc mà phải được thể hiện bằng hành động cụ thể, đúng đắn.
Tuy nhiên, hiện nay vẫn còn một số người sống thờ ơ, vô cảm, chỉ biết đến lợi ích cá nhân mà quên đi trách nhiệm với cộng đồng và đất nước. Điều đó đòi hỏi mỗi chúng ta phải tự nhìn nhận, điều chỉnh lối sống, nâng cao ý thức công dân.
Tóm lại, xây dựng và bảo vệ đất nước là nhiệm vụ chung của toàn xã hội, trong đó mỗi cá nhân đều giữ một vai trò quan trọng. Khi mỗi người sống có trách nhiệm, biết cống hiến và sẻ chia, đất nước sẽ ngày càng phát triển vững mạnh và bền lâu.
Câu 1.
Bài thơ được viết theo thể thơ thất ngôn tứ tuyệt Đường luật.
Câu 2.
- Trợ từ: kìa
- Từ tượng hình: cheo leo
Câu 3.
- Các từ ngữ thể hiện thái độ của nữ sĩ: ghé mắt, trông ngang, kìa, đứng cheo leo, há bấy nhiêu.
- Nhận xét: Thái độ của Hồ Xuân Hương là khinh bỉ, mỉa mai, chế giễu kẻ thù xâm lược thất bại, đồng thời thể hiện niềm tự hào dân tộc và ý thức đề cao khí phách anh hùng chân chính.
Câu 4.
- Biện pháp tu từ:
- Nói mỉa (“đền Thái thú”)
- Từ tượng hình (“cheo leo”)
- Tác dụng: Gợi lên hình ảnh ngôi đền nhỏ bé, lạc lõng, qua đó hạ thấp, châm biếm kẻ bại tướng xâm lược, làm nổi bật sự thất bại nhục nhã của Sầm Nghi Đống.
Câu 5.
Thông điệp của bài thơ:
→ Lên án kẻ xâm lược, đề cao lòng tự tôn dân tộc, ca ngợi chiến thắng oanh liệt của dân tộc Việt Nam, đồng thời thể hiện khát vọng bình đẳng giới và bản lĩnh cá nhân của người phụ nữ.
Trong xã hội hiện đại, giới trẻ được xem là lực lượng nòng cốt, là chủ nhân tương lai của đất nước. Tuy nhiên, bên cạnh nhiều bạn trẻ sống có lý tưởng, có ước mơ và trách nhiệm, vẫn còn một bộ phận giới trẻ đang có lối sống vô trách nhiệm, gây ra nhiều hệ lụy đáng lo ngại cho bản thân, gia đình và xã hội.
Lối sống vô trách nhiệm trước hết thể hiện ở thái độ thờ ơ với bản thân. Nhiều bạn trẻ sống buông thả, lười học tập, không có mục tiêu rõ ràng, sa đà vào mạng xã hội, trò chơi điện tử, hưởng thụ trước mắt mà không nghĩ đến tương lai. Không ít người coi việc học là nghĩa vụ bắt buộc chứ không phải cơ hội để hoàn thiện chính mình. Bên cạnh đó, sự vô trách nhiệm còn thể hiện ở cách ứng xử với gia đình và cộng đồng, như thiếu lễ phép với cha mẹ, vô cảm trước khó khăn của người khác, sẵn sàng vi phạm nội quy, pháp luật vì lợi ích cá nhân.
Nguyên nhân của lối sống này xuất phát từ nhiều phía. Một số bạn trẻ thiếu sự định hướng đúng đắn từ gia đình, được nuông chiều quá mức nên hình thành thói quen sống ích kỉ. Mặt khác, tác động tiêu cực của mạng xã hội khiến nhiều người chạy theo lối sống ảo, thích thể hiện bản thân nhưng ngại cố gắng. Ngoài ra, bản thân người trẻ chưa ý thức đầy đủ về trách nhiệm và giá trị của mình, dẫn đến lối sống dễ dãi, thiếu kỉ luật.
Hậu quả của lối sống vô trách nhiệm là vô cùng nghiêm trọng. Trước hết, người trẻ sẽ đánh mất tương lai của chính mình, thiếu kỹ năng, thiếu bản lĩnh để đối mặt với cuộc sống. Gia đình phải gánh chịu nỗi lo lắng, thất vọng, còn xã hội thì mất đi nguồn nhân lực chất lượng. Nếu tình trạng này kéo dài, nó sẽ ảnh hưởng tiêu cực đến sự phát triển bền vững của đất nước.
Trước thực trạng đó, mỗi bạn trẻ cần tự nhìn nhận và thay đổi bản thân. Hãy sống có mục tiêu, biết chịu trách nhiệm với hành động và lựa chọn của mình. Gia đình và nhà trường cũng cần quan tâm, giáo dục, định hướng đúng đắn về nhân cách và lối sống. Đồng thời, xã hội cần tạo ra môi trường lành mạnh để giới trẻ được học tập, rèn luyện và cống hiến.
Tóm lại, lối sống vô trách nhiệm của một bộ phận giới trẻ là vấn đề đáng báo động. Mỗi người trẻ cần hiểu rằng: sống có trách nhiệm không chỉ là bổn phận với bản thân mà còn là trách nhiệm với gia đình và tương lai của đất nước. Chỉ khi biết sống có trách nhiệm, giới trẻ mới thực sự trưởng thành và có thể đóng góp những giá trị tốt đẹp cho xã hội.
Câu 1.
Bài thơ được viết theo thể thơ thất ngôn bát cú Đường luật.
Câu 2.
Đối tượng trào phúng là chính tác giả (Nguyễn Khuyến) – một nhà nho tự giễu, tự cười mình, đồng thời phản ánh lớp trí thức đương thời.
Câu 3.
- “Làng nhàng” nghĩa là tầm thường, không nổi bật, không ra sao.
- Từ này thể hiện thái độ tự trào, chán ngán, tự nhận thức rõ sự bất lực và vị thế mờ nhạt của bản thân.
Câu 4.
- Nghệ thuật trào phúng: ẩn dụ + phóng đại + đối lập mỉa mai (cờ, bạc – những việc chưa tới hồi kết đã thua, đã bỏ).
- Tác dụng: châm biếm sự bất tài, thất bại, bất lực của bản thân trước cuộc đời, tạo tiếng cười cay đắng.
Câu 5.
Hai câu thơ thể hiện sự tự ý thức sâu sắc và mâu thuẫn nội tâm: tác giả chán chính mình nhưng vẫn mang danh hiệu, công danh → nỗi đau của kẻ có hư danh mà không thực quyền, không cống hiến được.
Câu 6.
Từ thông điệp bài thơ, giới trẻ ngày nay cần:
- Không chạy theo hư danh,
- Rèn luyện tri thức, nhân cách và bản lĩnh,
- Hành động thiết thực, sống có trách nhiệm để cống hiến và xây dựng quê hương, đất nước.