Cũng được á, nhưng mà mình góp ý 1 xíu là lặp từ hơi nhiều á, nên thành ra mình đọc hơi ko đc tự nhiên cho lắm (ykr)💝

a) \(A B C D\) là hình bình hành nên hai đường chéo \(A C , B D\) cắt nhau tại \(O\) là trung điểm của mỗi đường.

Xét \(\Delta O B M\) và \(\Delta O D P\) có:

     \(O B = O D\) ( giả thiết)

     \(\hat{O B M} = \hat{O D P}\) (so le trong)

     \(\hat{B O M} = \hat{D O P}\) (đối đỉnh)

Vậy \(\Delta O B M = \Delta O D P\) (g.c.g)

Suy ra \(O M = O P\) (hai cạnh tương ứng)

Chứng minh tương tự \(\Delta O A Q = \Delta O C N\) (g.c.g) suy ra \(O Q = O N\) (hai cạnh tương ứng)

\(M N P Q\) có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.

b) Hình bình hành \(M N P Q\) có hai đường chéo \(M P ⊥ N Q\) nên là hình thoi.

a) \(A B C D\) là hình bình hành nên \(A B = D C\) suy ra \(\frac{1}{2} A B = \frac{1}{2} D C\)

Do đó \(A M = B M = D N = C N\).

Tứ giác \(A M C N\) có \(A M\) // \(N C , A M = N C\) nên là hình bình hành.

Lại có \(\Delta A D C\) vuông tại \(A\) có \(A N\) là đường trung tuyến nên \(A N = \frac{1}{2} D C = D N = C N\).

Hình bình hành \(A M C N\) có hai cạnh kề bằng nhau nên là hình thoi, khi đó hai đường chéo \(A C , M N\) vuông góc với nhau.

Tứ giác \(A M C N\) là hình thoi.

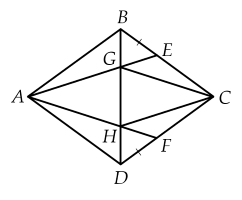
Ta có \(A B C D\) là hình thoi nên \(A C ⊥ B D\) tại trung điểm của mỗi đường nên \(B D\) là trung trực của \(A C\)

Suy ra \(G A = G C , H A = H C\) \(\left(\right. 1 \left.\right)\)

Và \(A C\) là trung trực của \(B D\) suy ra \(A G = A H , C G = C H\) \(\left(\right. 2 \left.\right)\)

Từ \(\left(\right. 1 \left.\right) , \left(\right. 2 \left.\right)\) suy ra \(A G = G C = C H = H A\) nên \(A G C H\) là hình thoi.

a) Với \(x \neq \pm 3\) ta có:

\(A = \frac{x + 15}{x^{2} - 9} + \frac{2}{x + 3} = \frac{x + 15}{\left(\right. x + 3 \left.\right) \left(\right. x - 3 \left.\right)} + \frac{2}{x + 3}\)

\(= \frac{x + 15 + 2 \left(\right. x - 3 \left.\right)}{\left(\right. x + 3 \left.\right) \left(\right. x - 3 \left.\right)}\)

\(= \frac{x + 15 + 2 x - 6}{\left(\right. x + 3 \left.\right) \left(\right. x - 3 \left.\right)}\)

\(= \frac{3 x + 9}{\left(\right. x + 3 \left.\right) \left(\right. x - 3 \left.\right)}\)

\(= \frac{3 \left(\right. x + 3 \left.\right)}{\left(\right. x + 3 \left.\right) \left(\right. x - 3 \left.\right)} = \frac{3}{x - 3}\)

Vậy với \(x \neq \pm 3\) thì \(A = \frac{3}{x - 3} .\)

b) Với \(x \neq \pm 3\), để \(A = \frac{- 1}{2}\) thì \(\frac{3}{x - 3} = \frac{- 1}{2}\)

Suy ra \(- x + 3 = 6\)

Do đó \(x = - 3\) (không thỏa mãn)

Vậy không có giá trị nào của \(x\) để \(A = \frac{- 1}{2} .\)

c) Với \(x \neq \pm 3\), để \(A\) nguyên thì \(\frac{3}{x - 3} \in \mathbb{Z}\), tức \(x - 3 \in\) Ư\(\left(\right. 3 \left.\right)\)

Mà Ư \(\)\(\left(\right.3\left.\right)={\pm1;\pm3\left.\right.}\), ta có bảng sau:

Các giá trị \(x\) tìm được ở trên đều thỏa mãn điều kiện \(x \neq \pm 3\) và \(x\) là số tự nhiên.

Vậy x ∈ {0; 2; 4; 6}.

\(\)

a) Xét tứ giác \(A B C D\) có \(\hat{A} + \hat{B} + \hat{C} + \hat{D} = 36 0^{\circ}\)

Áp dụng tính chất dãy tỉ số bằng nhau \(\frac{\hat{A}}{1} = \frac{\hat{B}}{2} = \frac{\hat{C}}{3} = \frac{\hat{D}}{4} = \frac{\hat{A} + \hat{B} + \hat{C} + \hat{D}}{1 + 2 + 3 + 4} = \frac{36 0^{\circ}}{10} = 3 6^{\circ}\).

Vậy \(\hat{B} = 3 6^{\circ} . 2 = 7 2^{\circ} .\)

b) Áp dụng định lí Pythagore vào tam giác \(A B C\) vuông tại \(A\) ta có: \(B C^{2} = A C^{2} + A B^{2}\)

Suy ra \(BC=\sqrt{A C^{2} + A B^{2}}=\sqrt{\left(15,5\right)^2+7^2}\approx17\) (cm).

Vì \(1\) inch \(\approx 2 , 54\) cm nên chiếc điện thoại theo hình vẽ có: \(\frac{17}{2 , 54} \approx 7\) inch.

a) \(10 x^{2} \left(\right. 2 x - y \left.\right) + 6 x y \left(\right. y - 2 x \left.\right)\)

\(= 10 x^{2} \left(\right. 2 x - y \left.\right) - 6 x y \left(\right. 2 x - y \left.\right)\)

\(= \left(\right. 2 x - y \left.\right) \left(\right. 10 x^{2} - 6 x y \left.\right)\)

\(= 2 x \left(\right. 2 x - y \left.\right) \left(\right. 5 x - 3 y \left.\right)\).​

b) \(x^{2} - 2 x + 1 - y^{2}\)

\(= \left(\right. x^{2} - 2 x + 1 \left.\right) - y^{2}\)

\(=\left(x-1\right)^2-y^2\)

\(= \left(\right. x - 1 - y \left.\right) \left(\right. x - 1 + y \left.\right) .\)

Diện tích cạnh đáy của hình chóp là:

\(\frac{3.1280}{15}=256\) (cm\(^{2}\))

Độ dài cạnh đáy của hình chóp là:

\(S = a^{2}\) nên \(a = \sqrt{256} = 16\) (cm)

Vậy độ dài cạnh đáy của hình chóp là \(16\) cm.

a) Giá tiền của \(x\) kg vải, \(y\) kg cam và \(z\) kg nho lần lượt là: \(45 x\); \(62 y\) và \(85 z\) (nghìn đồng).

Tổng số tiền bác Đô phải trả là

\(T = \left(\right. 45 x + 62 y + 85 z \left.\right) . 1 000\) (đồng).

b) Thay \(x = 1 , 5\); \(y = 3\) và \(z = 2\) vào \(\left(\right. 45 x + 62 y + 85 z \left.\right) . 1 000\) ta được

\(T = \left(\right. 45.1 , 5 + 62.3 + 85.2 \left.\right) . 1 000 = 423 500\) (đồng).

A=5+2xy+14y−x^2−5y^2−2x.

\(= - \left(\right. x^{2} + y^{2} + 1 - 2 x y - 2 y + 2 x \left.\right) - \left(\right. 4 y^{2} - 12 y + 9 \left.\right) + 15\)

\(=-\left(x-y+1\right)^2-\left(2y-3\right)^2+15\leq15\)

Suy ra giá trị lớn nhất của \(A = 15\) khi và chỉ khi:

\(x - y = - 1\) và \(2 y - 3 = 0\)

Suy ra \(x = \frac{1}{2}\) và \(y = \frac{3}{2}\).