Ta có \(4x^8-2x^7+x^6-3x^4+x^2-x+1\)

=\(x^6\left(x-1\right)^2+3\left(x^4-\frac12\right)^2+\left(x-\frac12\right)^2>0\forall x\) (đpcm)

ta đặt  \(t = \left(\right. x - 1 \left.\right) \left(\right. x - 4 \left.\right) = x^{2} - 5 x + 4\) thì 

\(\left(\right. x - 2 \left.\right) \left(\right. x - 3 \left.\right) = x^{2} - 5 x + 6 = t + 2\)

từ đó \(\left(\right. x - 1 \left.\right) \left(\right. x - 2 \left.\right) \left(\right. x - 3 \left.\right) \left(\right. x - 4 \left.\right) + 1\)

\(= t \left(\right. t + 2 \left.\right) + 1 = t^{2} + 2 t + 1 = \left(\right. t + 1 \left.\right)^{2} \geq 0\)\(\)

Vậy (x−1)(x−2)(x−3)(x−4)+1≥0.

+)Nếu \(x < 1\) thì \(x^{8} - x^{7} + x^{2} - x + 1\)

\(= x^{8} + x^{2} \left(\right. 1 - x^{5} \left.\right) + \left(\right. 1 - x \left.\right) > 0\).

+)Nếu \(x \geq 1\) thì \(x^{8} - x^{7} + x^{2} - x + 1\)

\(= x^{7} \left(\right. x - 1 \left.\right) + x \left(\right. x - 1 \left.\right) + 1 > 0\).

Vậy phương trình đã cho luôn lớn hơn 0 với mọi giá trị \(x\)

Ta có \(x + y = 1\) nên \(\left(\right. 1 + \frac{1}{x} \left.\right) \left(\right. 1 + \frac{1}{y} \left.\right) - 9\)

\(= \frac{\left(\right. x + 1 \left.\right) \left(\right. y + 1 \left.\right) - 9 x y}{x y} = \frac{2 - 8 x y}{x y}\)  

\(= \frac{2 \left(\right. 1 - 4 x y \left.\right)}{x y} = \frac{2 \left(\right. \left(\right. x + y \left.\right)^{2} - 4 x y \left.\right)}{x y}\)

\(= \frac{2 \left(\right. x - y \left.\right)^{2}}{x y} \geq 0\)

suy ra \(\left(\right.1+\frac{1}{x}\left.\right)\left(\right.1+\frac{1}{y}\left.\right)\ge9\)

Dấu đẳng thức xảy ra khi và chỉ khi \(x = y = \frac{1}{2}\).

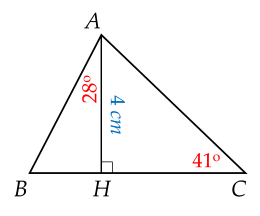
a) Xét tam giác \(A B H\) vuông tại \(H\), ta có \(H B = A H . tan ⁡ \hat{B A H} = 4. tan ⁡ 2 8^{\circ} \approx 2 , 1\) (cm)

Vì  \(A H C\) vuông tại \(H\) nên \(H C = A H . cot ⁡ \hat{C} = 4. cot ⁡ 4 1^{\circ} \approx 4 , 6\) (cm)

b) Xét tam giác \(A B H\) vuông tại \(H\), ta có

\(cos ⁡ \hat{B A H} = \frac{A H}{A B}\) hay \(A B = \frac{A H}{cos ⁡ \hat{B A H}} = \frac{4}{cos ⁡ 28 ^{\circ}} \approx 4 , 5\) (cm)

Vì tam giác \(A H C\) vuông tại \(H\) nên \(sin ⁡ \hat{C} = \frac{A H}{A C}\) hay \(A C = \frac{A H}{sin ⁡ \hat{C}} = \frac{4}{sin ⁡ 4 1^{\circ}} \approx 6 , 1\) (cm).

Kẻ đường cao \(A H ⊥ B C\).

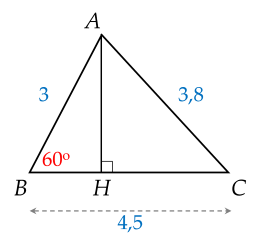
Xét \(\Delta A B H\) vuông tại \(H\) có \(A H = A B . sin ⁡ \hat{B} = 3. sin ⁡ 6 0^{\circ} \approx 2 , 6\) (cm)

Tương tự, xét \(B H = A B . cos ⁡ \hat{B} = 3. cos ⁡ 6 0^{\circ} = 1 , 5\) (cm)

Mà \(H C = B C - H B = 4 , 5 - 1 , 5 = 3 , 0\) (cm)

Theo định lí Pythagore trong \(\Delta ABH\) vuông tại \(H\) ta có \(A B^{2} = B H^{2} + A H^{2} = 3^{2} + 2 , 6^{2} = 15 , 76\) (cm) (Nhầm tam giác rồi)

Suy ra \(A B = \sqrt{15 , 76} \approx 4 , 0\) (cm) (đề cho rồi mà?)

Xét \(\Delta A H C\) vuông tại \(H\) ta có \(tan⁡\hat{A C H}=\frac{A H}{H C}\approx\frac{2 , 6}{3 , 0}=\frac{13}{15}\)

suy ra \(\hat{ACH}\) = 40 độ 55 phút

Do \(\hat{A} = 18 0^{\circ} - \hat{B} - \hat{C} = 18 0^{\circ} - \left(\right. 6 0^{\circ} + 4 0^{\circ} 5 5^{'} \left.\right) = 7 9^{\circ} 5^{'}\).

Vẽ \(A H ⊥ B C\).

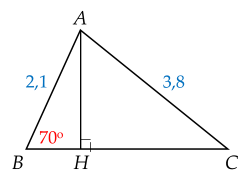
Xét \(\Delta ABH\) vuông tại \(H\) ta có:

 \(A H = A B . sin ⁡ \hat{B} = 2 , 1. sin ⁡ 7 0^{\circ} \approx 1 , 97\)

 \(B H = A B . cos ⁡ \hat{B} = 2 , 1. cos ⁡ 7 0^{\circ} \approx 0 , 72\)

Xét \(\Delta A H C\) vuông tại \(H\) ta có

\(sin⁡\hat{C}=\frac{A H}{A C}\approx\frac{1 , 97}{3 , 8}\)

Do đó \(\hat{C} \approx 3 1^{\circ} 1 4^{'}\)

Mà \(\hat{A} = 18 0^{\circ} - \left(\right. 7 0^{\circ} + 3 1^{\circ} 1 4^{'} \left.\right) = 7 8^{\circ} 4 6^{'}\)

Ta có \(H C = A C . cos ⁡ \hat{C} \approx 3 , 80. cos ⁡ 3 1^{\circ} 1 4^{'} \approx 3 , 25\) (cm)

Mà \(B C = B H + H C = 0 , 72 + 3 , 25 = 3 , 97\) (cm)

+)Xét \(\Delta ABC\) vuông tại \(\hat{A}\) ta có;

 \(\hat{A} = 180 ^{\circ} - \hat{B} - \hat{C} = 7 5^{\circ}\)

+)Kẻ đường cao \(B H\) (H thuộc AC)

Xét \(\Delta B C H\) vuông tại \(H\), ta có:

\(B H = B C . sin ⁡ \hat{C} = 4 , 2. sin ⁡ 4 0^{\circ} \approx 2 , 70\) (cm)

Tương tự, xét \(\Delta A B H\) vuông tại \(H\), ta có:

\(A B = \frac{B H}{sin ⁡ \hat{A}} = \frac{2 , 70}{sin ⁡ 7 5^{\circ}} \approx 2 , 8\) (cm)

+)Ta có \(AC=AH+CH=BH.\left(\right.cot⁡\hat{A}+cot⁡\hat{C}\left.\right)\approx2,70.\left(\right.cot⁡75^{\circ}+cot⁡40^{\circ}\left.\right)\approx3,9\) (cm)

Ta có \(\hat{A} = 18 0^{\circ} - \hat{B} - \hat{C} = 7 0^{\circ}\).

Kẻ đường cao \(A H\) (H thuộc BC)

Xét \(\Delta A B H\) vuông tại \(H\), ta có \(A H = A B . sin ⁡ \hat{B} = 2 , 8. sin ⁡ 6 5^{\circ} \approx 2 , 54\) (cm).

Tương tự \(B H = A B . cos ⁡ \hat{B} = 2 , 8. cos ⁡ 6 5^{\circ} \approx 1 , 18\) (cm).

Mặt khác do giả thiết suy ra tam giác \(H A C\) vuông cân tại \(H\) nên \(H A = H C\).

Do đó \(B C \approx 2 , 54 + 1 , 18 = 3 , 7\) (cm).

Xét \(\Delta A H C\) vuông tại \(H\), ta có \(A C = \frac{H A}{sin ⁡ C} = \frac{2 , 54}{sin ⁡ 4 5^{\circ}} \approx 3 , 6\) (cm).

Giả thiết đã cho chia cả hai vế cho abc ta có \(\frac{1}{a} + \frac{1}{b} + \frac{1}{c} + \frac{1}{a b} + \frac{1}{b c} + \frac{1}{c a} = 6\). (1)

Mặt khác ta có \(\left(\right. \frac{1}{a} - 1 \left.\right)^{2} \geq 0\)

\(\frac{1}{a^{2}} + 1 \geq \frac{2}{a}\) nên 

\(\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} \geq 2 \left(\right. \frac{1}{a} + \frac{1}{b} + \frac{1}{c} \left.\right) - 3\) (2)

Lại có \(\frac{1}{a^{2}} + \frac{1}{b^{2}} \geq \frac{2}{a b}\) nên 

\(2 \left(\right. \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} \left.\right) \geq 2 \left(\right. \frac{1}{a b} + \frac{1}{b c} + \frac{1}{c a} \left.\right)\) (3)

Cộng (2) và (3) theo vế  và sử dụng (1)  ta có    

\(3 \left(\right. \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} \left.\right) \geq 2 \left(\right. \frac{1}{a b} + \frac{1}{b c} + \frac{1}{c a} + \frac{1}{a} + \frac{1}{b} + \frac{1}{c} \left.\right) - 3 = 2.6 - 3 = 9\) 

Suy ra \(\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} \geq 3\).