Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra số 4 SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Trong mặt phẳng cho ba điểm tùy ý A,B và C. Khẳng định nào sau đây đúng?
Cho tam giác ABC. Gọi M,N,P lần lượt là trung điểm của AB,BC,CA.

Vectơ tổng MP+NP bằng
Giá trị của tan30∘+cot150∘ là
Tập nghiệm của phương trìnhx2−2x=2x−x2 là
Bảng xét dấu trong hình vẽ là của tam thức bậc hai nào sau đây?
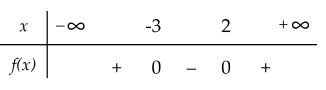
Cho A=(−2;1),B=[−3;5]. Khi đó A∩B là tập hợp nào sau đây?
Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
Giá trị của hàm số y=2x+3 tại x=4 là
Tập xác định của hàm số y=x−1+2−x là
Cho hai vectơ a; b khác vectơ 0 thỏa mãn a.b=21−a.b. Khi đó góc giữa hai vectơ a; b bằng
Cho tam giác ABC với AD là đường phân giác trong. Biết AB=5, BC=6, CA=7. Khẳng định nào sau đây đúng?
Tập nghiệm của bất phương trình (x−2)2−6x+21>0 là
Cho tam giác ABC có trực tâm H và M là trung điểm BC.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) HA.CB=1. |
|
| b) BH.CA=0. |
|
| c) MH.MA=4BC2. |
|
| d) MH2+MA2=AH2+2BC2. |
|
Cho hàm số y=x2−4x+1.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Tọa độ đỉnh I(2;3). |
|
| b) Phương trình trục đối xứng parabol: x=3. |
|
| c) Bề lõm parabol hướng lên. |
|
d) Đồ thị parabol như hình vẽ:  . .
|
|
Cho hàm số y=m+1m−2x+2m−1.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Với m>2, hàm số đồng biến trên R. |
|
| b) Với m<1, hàm số nghịch biến trên R. |
|
| c) Có 2 giá trị nguyên của tham số m để hàm số đã cho nghịch biến trên R. |
|
| d) Có 4 giá trị của tham số m để giá trị lớn nhất của hàm số trên [−2;3] bằng 5. |
|
Cho hàm số y=x2−4x.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Tập xác định của hàm số là D=R. |
|
| b) Đồ thị của hàm số có đỉnh I(2;−4). |
|
| c) Đồ thị của hàm số có trục đối xứng là đường thẳng x=−1. |
|
| d) Tọa độ giao điểm của đồ thị hàm số với trục Ox là O(0;0),B(4;0). |
|
Trên biển Đông, một tàu chuyển động đều từ vị trí A theo hướng N20∘W với vận tốc 30 km/h. Sau 5 giờ, tàu đến được vị trí B. A cách B bao nhiêu ki lô mét và về hướng S20∘E so với B?
Trả lời:
Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y=x2−2mx−2m+31 có tập xác định là R?
Trả lời:
Thầy Đô có 45 m lưới muốn rào một mảnh vườn hình chữ nhật để trồng rau, biết rằng một cạnh là tường, Thầy Đô chỉ cần rào 3 cạnh còn lại của hình chữ nhật để làm vườn.

Có bao nhiêu giá trị nguyên của x (trong hình vẽ) để diện tích mảnh vườn không bé hơn 100 m2?
Trả lời:
Gọi S là tập hợp tất cả các giá trị dương của tham số m để giá trị nhỏ nhất của hàm số y=f(x)=4x2−4mx+m2−2m trên đoạn [−2;0] bằng 3. Tổng các phần tử của S bằng bao nhiêu?
Trả lời:
Có hai địa điểm A,B cùng nằm trên một tuyến quốc lộ thẳng. Khoảng cách giữa A và B là 30,5 km. Một xe máy xuất phát từ A lúc 7 giờ theo chiều từ A đến B. Lúc 9 giờ, một ô tô xuất phát từ B chuyển động thẳng đều với vận tốc 80 km/h theo cùng chiều với xe máy. Chọn A làm mốc, chọn thời điểm 7 giờ làm mốc thời gian và chọn chiều từ A đến B làm chiều dương. Phương trình chuyển động của xe máy là y=2t2+36t, trong đó y tính bằng ki-lô-mét, t tính bằng giờ. Đến lúc ô tô đuổi kịp xe máy thì hai xe dừng lại, vị trí đó cách điểm B bao nhiêu km?
Trả lời:
Một xưởng sản xuất hai loại sản phẩm là sản phẩm loại I và sản phẩm loại II:
▪️ Mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, thu lời (lãi) được 40 nghìn đồng.
▪️ Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, thu lời được 30 nghìn đồng.
Xưởng có 200 kg nguyên liệu và 1200 giờ làm việc tối đa. Để có mức tiền lãi cao nhất, xưởng cần sản xuất a sản phẩm loại I và b sản phẩm loại II. Tính a+b.
Trả lời:
