olm
Đăng nhập Đăng ký

Bài học cùng chủ đề

Báo cáo học liệu
Mua học liệu
Mua học liệu:
  • Số dư ví của bạn: 0 coin - 0 Xu
  • Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 6) SVIP

Tải ma trận

Yêu cầu đăng nhập!

Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!

Câu 1 (1đ):

Cho tam giác ABCABC có AB=33 AB=3\sqrt{3} và bán kính đường tròn ngoại tiếp R=3R=3. Số đo góc CC là

60∘60^\circ.
90∘90^\circ.
30∘30^\circ.
45∘45^\circ.
Câu 2 (1đ):

Giá trị của tan⁡45∘+cot⁡135∘ \tan 45^\circ + \cot 135^\circ bằng

2 2 .
0 0 .
3 \sqrt{3} .
1 1 .
Câu 3 (1đ):

Cho hệ bất phương trình {x>0x+3y+1≤0 \left\{ \begin{aligned} & x>0 \\ & x+\sqrt{3}y+1\le 0 \\ \end{aligned} \right. có tập nghiệm là S S . Khẳng định nào sau đây đúng?

(−1;5)∉S (-1;\sqrt{5})\notin S .
(1;−3)∈S (1;-\sqrt{3})\in S .
(−4;3)∈S (-4;\sqrt{3})\in S .
(1;−1)∈S (1;-1)\in S .
Câu 4 (1đ):

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

y<5y\lt 5.
x2+y2≥0x^2+y^2\ge 0.
y3−27>0y^3-27>0.
(x−2y)(x+y)≥1(x-2y )(x+y )\ge 1.
Câu 5 (1đ):

Sử dụng các kí hiệu đoạn, khoảng, nửa khoảng để viết tập hợp A={x∈R ∣ x≤1}A=\Big\{x \in \mathbb{R} \, \big| \, x \le 1 \Big\} ta có

A=(−∞;1]A=\left(-\infty ; 1 \right].
A=(−∞;1)A=\left(-\infty ; 1 \right).
A=(1;+∞)A=\left(1 ; +\infty \right).
A=[1;+∞)A=\left[1 ; +\infty \right).
Câu 6 (1đ):

Tập hợp nào dưới đây có đúng một tập hợp con?

{∅}\{ \varnothing \}.
{∅, x}\{ \varnothing,\,x \}.
{x}\{ x\}.
∅\varnothing .
Câu 7 (1đ):

Cho hai mệnh đề: PP: "3030 không chia hết cho 55" và QQ: "π<3,15\pi < 3,15". Khẳng định nào sau đây đúng?

P‾\overline{P} đúng, Q‾\overline{Q} sai.
P‾\overline{P} sai, Q‾\overline{Q} đúng.
P‾\overline{P} đúng, Q‾\overline{Q} đúng.
P‾\overline{P} sai, Q‾\overline{Q} sai.
Câu 8 (1đ):

Cho tam giác ABC ABC với BC=a, AC=b, AB=c BC=a, \, AC=b, \, AB=c , bán kính đường tròn ngoại tiếp R R . Khẳng định nào sau đây đúng?

a=2Rcos⁡A a=2R\cos A .
a=Rsin⁡A a=R\sin A .
a=2Rtan⁡A a=2R\tan A .
a=2Rsin⁡A a=2R\sin A .
Câu 9 (1đ):

Trên nửa đường tròn đơn vị, cho góc α \alpha như hình vẽ:

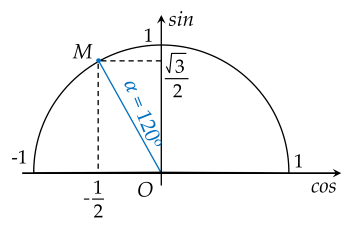
loading...

Các giá trị lượng giác của góc α \alpha là

sin⁡α=32 \sin \alpha =\dfrac{\sqrt3}2 ; cos⁡α=−12 \cos \alpha =-\dfrac12 ; tan⁡α=−3 \tan \alpha =-\sqrt3 ; cot⁡α=−33 \cot \alpha =-\dfrac{\sqrt3}3 .
sin⁡α=32 \sin \alpha =\dfrac{\sqrt3}2 ; cos⁡α=12 \cos \alpha =\dfrac12 ; tan⁡α=1 \tan \alpha =1 ; cot⁡α=1 \cot \alpha =1 .
sin⁡α=32 \sin \alpha =\dfrac{\sqrt3}2 ; cos⁡α=−12 \cos \alpha =-\dfrac12 ; tan⁡α=1 \tan \alpha =1 ; cot⁡α=1 \cot \alpha =1 .
sin⁡α=−32 \sin \alpha =-\dfrac{\sqrt3}2 ; cos⁡α=12 \cos \alpha =\dfrac12 ; tan⁡α=−3 \tan \alpha =-\sqrt3 ; cot⁡α=−33 \cot \alpha =-\dfrac{\sqrt3}3 .
Câu 10 (1đ):

Trong tam giác ABC ABC có bán kính đường tròn ngoại tiếp R R , hệ thức nào sau đây sai?

sin⁡C=c.sin⁡Aa \sin C=\dfrac{c.\sin A}{a} .
b=R.tan⁡B b=R.\tan B .
a=2R.sin⁡A a=2R.\sin A .
a=b.sin⁡Asin⁡B a=\dfrac{b.\sin A}{\sin B} .
Câu 11 (1đ):

Cho biết cos⁡α+sin⁡α=13. \cos \alpha +\sin \alpha =\dfrac13. Giá trị của P=tan⁡2α+cot⁡2α P=\sqrt{\tan^2 \alpha + \cot^2 \alpha} bằng 

74. \dfrac{7}{4}.
54. \dfrac{5}{4}.
94. \dfrac{9}{4}.
114. \dfrac{11}{4}.
Câu 12 (1đ):

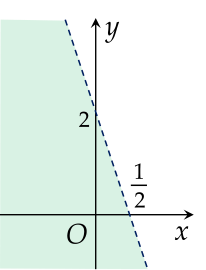
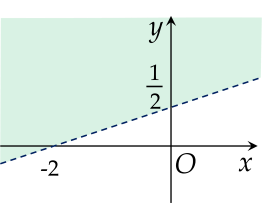
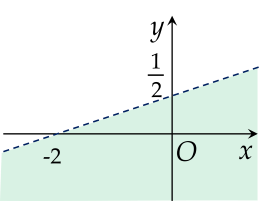
Miền nghiệm của bất phương trình x−4y+2<0 x-4y+2<0 là phần tô màu (không bao gồm đường thẳng nét đứt) hình vẽ nào dưới đây?

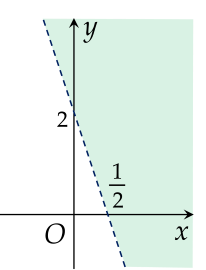
loading... 
loading... 
loading... 
loading... 
Câu 13 (1đ):

Cho hệ bất phương trình {3−y<02x−3y+1>0\left\{ \begin{aligned}& 3-y\lt 0 \\& 2x-3y+1>0 \\\end{aligned} \right..

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Hệ đã cho không phải là hệ bất phương trình bậc nhất hai ẩn.
b) B(4;3)B(4;3 ) là một điểm thuộc miền nghiệm của hệ.
c) C(7;4)C(7;4 ) là một điểm thuộc miền nghiệm của hệ.
d) Miền không tô màu (không kể bờ) như hình vẽ là miền nghiệm của hệ .
Câu 14 (1đ):

Cho hai tập hợp: A=(−3;5], B=(2;+∞)A=(-3;5],\,B=(2;+\infty).

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) A\B=(2;5]A\backslash B=(2;5].
b) A∪B=(−3;+∞)A\cup B=(-3;+\infty).
c) A∩B=(2;5]A\cap B=(2;5].
d) CRB=(−∞;2)C_{\mathbb{R}}B=(-\infty ;2).
Câu 15 (1đ):

Cho P(x) P(x) : "x2−x−2=0 x^2-x-2=0 " với x x là các số thực.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) x=0 x=0 thì P(x) P(x) là mệnh đề đúng.
b) P(−1) P(-1) là mệnh đề sai.
c) P(x) P(x) luôn là mệnh đề sai với x x là các số thực bất kì.
d) P(2) P(2) là mệnh đề đúng.
Câu 16 (1đ):

Cho các hệ bất phương trình sau:{x−2y≤05x−y≥−4x+2y≤5 \left\{ \begin{aligned} &x-2y \le 0 \\&5x-y \ge -4 \\&x+2y \le 5 \\ \end{aligned} \right. , {−x−y<4−x+2y>−2x+y<8x≥−6y≤6 \left\{ \begin{aligned} &-x-y<4 \\&-x+2y>-2 \\&x+y<8 \\&x\ge -6 \\&y\le 6 \\ \end{aligned} \right. .

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Miền nghiệm của hệ bất phương trình {x−2y≤05x−y≥−4x+2y≤5 \left\{ \begin{aligned} &x-2y\le 0 \\ &5x-y\ge -4 \\ &x+2y\le 5 \\ \end{aligned} \right. là miền tam giác.
b) Điểm M(1;1) M(1;1) thỏa mãn miền nghiệm của hệ bất phương trình {x−2y≤05x−y≥−4x+2y≤5 \left\{ \begin{aligned}&x-2y\le 0 \\&5x-y\ge -4 \\&x+2y\le 5 \\ \end{aligned} \right. .
c) Miền nghiệm của hệ bất phương trình {−x−y<4−x+2y>−2x+y<8x≥−6y≤6 \left\{ \begin{aligned}&-x-y<4 \\&-x+2y>-2 \\&x+y<8 \\&x\ge -6 \\&y\le 6 \\ \end{aligned} \right. là miền tứ giác.
d) Điểm O(0;0) O(0;0) không thỏa mãn miền nghiệm của hệ bất phương trình {−x−y<4−x+2y>−2x+y<8x≥−6y≤6 \left\{ \begin{aligned}&-x-y<4 \\&-x+2y>-2 \\&x+y<8 \\&x\ge -6 \\& y\le 6 \\ \end{aligned} \right. .
Câu 17 (1đ):

Lớp 10A có 21 21 em thích học Toán, 19 19 em thích học Văn và có 18 18 em thích học tiếng Anh. Trong số đó có 9 9 em thích học cả Toán lẫn Văn, 7 7 em thích học cả Văn lẫn tiếng Anh, 6 6 em thích học cả Toán lẫn tiếng Anh và có 4 4 em thích học cả ba môn Toán, Văn, Anh, không có em nào không thích một trong ba môn học trên. Trong lớp 10A có bao nhiêu học sinh?

Trả lời:

Câu 18 (1đ):

Cho hai tập khác rỗng A=[0;5] A=\left[ 0;5 \right] ; B=(2a;3a+1] B=\left(2a;3a+1 \right] . Có bao nhiêu giá trị nguyên của a a để A∩B≠∅ A\cap B\ne \varnothing ?

Trả lời:

Câu 19 (1đ):

Bạn Lan mang theo đúng 15 15 nghìn đồng để đi mua vở. Vở loại A A có giá 3 000 3 \, 000 đồng một cuốn, vở loại B B có giá 4 000 4 \, 000 đồng một cuốn. Bạn Lan có thể mua nhiều nhất bao nhiêu quyển vở sao cho bạn có cả hai loại vở?

Trả lời:

Câu 20 (1đ):

Tìm giá trị nhỏ nhất của biểu thức F(x;y)=x−y F(x;y)=x-y với điều kiện {x≥0y≥0x+y−3≤0 \left\{ \begin{aligned}&x \ge 0 \\&y \ge 0 \\&x+y-3 \le 0 \\ \end{aligned} \right. .

Trả lời:

Câu 21 (1đ):

Một phân xưởng may áo vest và quần âu để chuẩn bị cho dịp cuối năm. Biết rằng may 11 áo vest hết 22 m vải và cần 2020 giờ; 11 quần âu hết 1,51,5 m vải và cần 55 giờ. Xí nghiệp được giao sử dụng không quá 900900 m vải và số giờ công không vượt quá 6 0006\,000 giờ. Theo khảo sát thị trường, số lượng quần bán không vượt quá 22 lần số lượng áo. Khi xuất ra thị trường, 11 chiếc áo lãi 350350 nghìn đồng, 11 chiếc quần lãi 100100 nghìn đồng. Phân xưởng cần may aa chiếc áo vest và bb chiếc quần âu để thu được tiền lãi cao nhất, với aa và bb là các số tự nhiên (biết thị trường tiêu thụ luôn đón nhận sản phẩm của xí nghiệp). Giá trị của biểu thức T=a−bT=a-b bằng bao nhiêu?

Trả lời:

Câu 22 (1đ):

Muốn đo chiều cao của một cái cây mà không thể đến được gốc cây, người ta lấy hai điểm MM, NN trên mặt đất có khoảng cách MN=5MN=5 m cùng thẳng hàng với gốc cây để đặt hai giác kế. Chân của giác kế có chiều cao MA=NB=1,2MA=NB=1,2 m. Lấy điểm DD trên thân cây sao cho AA, BB, DD thẳng hàng. Người ta đo được CAD^=α=36∘\widehat{CAD}=\alpha =36^\circ và CBD^=β=41∘\widehat{CBD}=\beta =41^\circ .

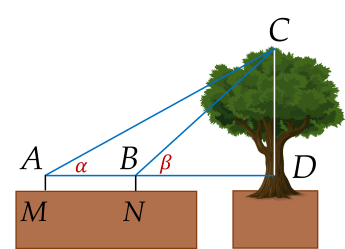
loading...

Tính chiều cao của cây. (Làm tròn kết quả đến hàng phần mười của đơn vị mét)

Trả lời:

OLM©2022OLM \copyright 2022
Truy vết IP log
Cảnh báo

Đây là bài thi, vui lòng bấm "Xác nhận" để tiếp tục làm bài!

Báo lỗi câu hỏi
Bạn đã gặp lỗi gì ở câu hỏi này, hãy mô tả vào ô bên dưới. Với mỗi lỗi thông báo đúng, OLM sẽ tặng bạn 1-3 ngày VIP!
Bạn có thể báo lỗi bằng hình ảnh tại đây!!!
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP