Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải chi tiết:
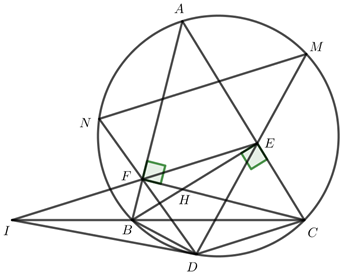
a) Chứng minh tứ giác AEHF và BCEF nội tiếp.
Ta có ∠AEH=∠AFH=90o⇒∠AEH=∠AFH=90o⇒ E, F thuộc đường tròn đường kính AH
⇒⇒ A, E, H, F cùng thuộc một đường tròn
⇒AEHF⇒AEHF là tứ giác nội tiếp (dhnb).
Ta có ∠BEC=∠BFC=90o⇒∠BEC=∠BFC=90o⇒ BCEF là tứ giác nội tiếp (dhnb)
b) Hai đường thẳng EF và BC cắt nhau tại I. Vẽ tiếp tuyến ID với (O)(O)(D là tiếp điểm, D thuộc cung nhỏ BC). Chứng minh ID2=IB.ICID2=IB.IC.
Xét ΔIBDΔIBD và ΔIDCΔIDC có:
∠I∠I chung
∠IDB=∠ICD∠IDB=∠ICD (ID là tiếp tuyến của (O)(O))
⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).
c) DE, DF cắt đường tròn (O)(O) tại M và N. Chứng minh NM // EF.
Xét ΔIBEΔIBE và ΔIFCΔIFC có:
∠I∠I chung
∠IEB=∠ICF∠IEB=∠ICF (BCEF là tứ giác nội tiếp)
⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF (kết hợp b)
⇒ID2=IE.IF⇒IDIE=IFID⇒ID2=IE.IF⇒IDIE=IFID
Xét ΔIDFΔIDF và ΔIEDΔIED có:
∠I∠I chung
IDIE=IFID(cmt)IDIE=IFID(cmt)
⇒ΔIDF∼ΔIED⇒∠IDF=∠IED⇒ΔIDF∼ΔIED⇒∠IDF=∠IED (2 góc tương ứng)
Mặt khác ∠IDF=∠NMD∠IDF=∠NMD (ID là tiếp tuyến của (O)(O)) ⇒∠IED=∠NMD⇒∠IED=∠NMD (tc)
Mà hai góc này ở vị trí đồng vị ⇒⇒ NM // EF.

1: góc ABP=1/2*sđ cung AP=90 độ
=>BP//CH
góc ACP=1/2*sđ cung AP=90 độ
=>CP//BH
mà BP//CH
nên BHCP là hình bình hành
=>BC cắt HP tại trung điểm của mỗi đường
=>M là trung điểm của HP

A B C O F H E D I K A' C' B' M N
a) Do BHCK là hình bình hành nên BH // KC \(\Rightarrow KC\perp AC\Rightarrow\widehat{ACK}=90^o\)
KB // CF \(\Rightarrow\widehat{ABK}=90^o\)
Hai tam giác vuông ABK và ACK chung cạnh huyền AK nên A, B, C, K cùng thuộc đường tròn đường kính AK. Vậy K thuộc đường tròn (O).
b) Do BHCK là hình bình hành nên I là trung điểm HK.
AK là đường kính nên \(\widehat{AA'K}=90^o\Rightarrow\) DI // A'K
Vậy DI là đường trung bình tam giác HA'K. Suy ra HD = DA'
Tương tự : HF = FC' ; HE = EB'
Ta có : \(\frac{AA'}{AD}+\frac{BB'}{BE}+\frac{CC'}{CF}=\frac{AD+DA'}{AD}+\frac{BE+EE'}{BE}+\frac{CF+FC'}{CF}\)
\(=1+\frac{DA'}{AD}+1+\frac{EB'}{BE}+1+\frac{FC'}{CF}=3+\left(\frac{DA'}{AD}+\frac{EB'}{BE}+\frac{FC'}{CF}\right)\)
\(=3+\left(\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}\right)=3+\left(\frac{S_{BHC}}{S_{ABC}}+\frac{S_{AHC}}{S_{ABC}}+\frac{S_{AHB}}{S_{ABC}}\right)\)
\(=3+\frac{S_{ABC}}{S_{ABC}}=3+1=4\)
Vậy nên \(\frac{AA'}{AD}+\frac{BB'}{BE}+\frac{CC'}{CF}=4\)
c) Ta thấy \(\widehat{AKC}=\widehat{ABC}=\widehat{AHF}\)
Vậy nên \(\Delta AFH\sim\Delta ACK\left(g-g\right)\Rightarrow\frac{AH}{AK}=\frac{AF}{AC}\) (1)
AFH và AEH là các tam giác vuông chung cạnh huyền AH nên AFHE là tứ giác nội tiếp.
Vậy thì \(\widehat{AFM}=\widehat{AHE}=\widehat{ACN}\)
Lại có \(\Delta AFH\sim\Delta ACK\Rightarrow\widehat{FAM}=\widehat{CAN}\)
Nên \(\Delta AFM\sim\Delta ACN\left(g-g\right)\Rightarrow\frac{AF}{AC}=\frac{AM}{AN}\) (2)
Từ (1) và (2) suy ra \(\frac{AH}{AK}=\frac{AM}{AN}\Rightarrow\frac{AH}{AM}=\frac{AK}{AN}\Rightarrow\) MN // HK (Định lý Talet đảo)

http://tailieu.metadata.vn/chi-tiet/-/tai-lieu/tuyen-tap-80-bai-toan-hinh-hoc-lop-9-pdf-17121.html
bạn tự vẽ hình nhé còn phần chứng minh để tui lo
a) để chứng minh 5 điểm này cùng nằm trên đường tròn thì bạn cần chứng minh 4 điểm A,K,F,E cùng nằm trên 1 đường tròn ( chứng minh tứ giác AKFE nội tiếp theo các cách chứng minh trong SGK toán 9 tập 2 trang 103 phần thứ 15) và bạn chứng minh 4 điểm này theo đúng hình vẽ mà bạn vẽ
sau đó chứng minh nốt K,E,F,H cùng nằm trên 1 đường tròn hoặc các điểm khác như : A,K,H,F ....... tùy hình vẽ (cách chứng minh giống như trên)
sau khi chứng minh đc 2 điều này thì => điều phải chứng minh ở phần a
b) để chứng minh 4 điểm này thẳng hàng thì có rất nhiều cách nhưng bạn nên chọn cách chứng minh 3 điểm M,H,S hoặc H,S,K , ..... cùng thẳng hàng sau đó => 4 điểm thẳng hàng
để chứng minh đc thì bạn nên xem hình vẽ và dữ kiện đã chứng minh ở phần a và suy ra những thứ cần thiết để có thể chứng minh đc cho phần b
bạn có thể chứng minh : ở 3 điểm đó có 3 góc mà khi cộng chúng lại với nhau sẽ bằng 180 độ => 3 điểm thẳng hàng
=> 4 điểm thẳng hàng
đây có thể là cách tốt nhất nhanh nhất mà mình nghĩ ra trong vòng vài phút mong bạn thông cảm thời gian của mình có hạn nên chỉ hướng dẫn đc tới đây ! .................

Để chứng minh ba điểm thẳng hàng trong bài toán hình học này, ta sử dụng kiến thức về tính chất trực tâm, trung điểm, đường tròn nội tiếp và hình học tổ hợp. Tóm tắt bài toán: nhọn, nội tiếp đường tròn (O), là các đường cao đồng quy tại trực tâm là giao điểm của và cắt (O) tại là trung điểm của Cần chứng minh: thẳng hàng. --- Hướng chứng minh: 1. Sử dụng tam giác nội tiếp và trực tâm: là đường thẳng nối hai chân đường cao từ và , nên nó là đường thẳng vuông góc với trục trung tuyến của tam giác . Giao điểm của và thường gọi là điểm phản trực tâm. 2. Đường thẳng cắt đường tròn (O) tại điểm thứ hai là : Vì nằm trên đường tròn, và là đường qua đỉnh và điểm đặc biệt, ta xem xét tính chất của đường Euler hoặc trục đối xứng trong các cấu hình đặc biệt. 3. Xét tam giác với trực tâm và trung điểm đáy: Trung điểm của , cùng với trực tâm , thường thẳng hàng với những điểm nằm trên đường trung trực của cạnh hoặc trục đối xứng. 4. Áp dụng định lý Pascal (nâng cao): Nếu bạn coi lục giác nội tiếp đường tròn gồm các điểm và áp dụng định lý Pascal, có thể suy ra tính thẳng hàng giữa ba điểm đặc biệt như . --- Kết luận: Ba điểm thẳng hàng do các tính chất hình học đặc biệt liên quan đến giao điểm của các đường cao, trung điểm cạnh đáy và điểm cắt đường tròn tại tiếp tuyến từ chân đường cao.
Để chứng minh ba điểm thẳng hàng trong bài toán hình học này, ta sử dụng kiến thức về tính chất trực tâm, trung điểm, đường tròn nội tiếp và hình học tổ hợp. Tóm tắt bài toán: nhọn, nội tiếp đường tròn (O), là các đường cao đồng quy tại trực tâm là giao điểm của và cắt (O) tại là trung điểm của Cần chứng minh: thẳng hàng. --- Hướng chứng minh: 1. Sử dụng tam giác nội tiếp và trực tâm: là đường thẳng nối hai chân đường cao từ và , nên nó là đường thẳng vuông góc với trục trung tuyến của tam giác . Giao điểm của và thường gọi là điểm phản trực tâm. 2. Đường thẳng cắt đường tròn (O) tại điểm thứ hai là : Vì nằm trên đường tròn, và là đường qua đỉnh và điểm đặc biệt, ta xem xét tính chất của đường Euler hoặc trục đối xứng trong các cấu hình đặc biệt. 3. Xét tam giác với trực tâm và trung điểm đáy: Trung điểm của , cùng với trực tâm , thường thẳng hàng với những điểm nằm trên đường trung trực của cạnh hoặc trục đối xứng. 4. Áp dụng định lý Pascal (nâng cao): Nếu bạn coi lục giác nội tiếp đường tròn gồm các điểm và áp dụng định lý Pascal, có thể suy ra tính thẳng hàng giữa ba điểm đặc biệt như . --- Kết luận: Ba điểm thẳng hàng do các tính chất hình học đặc biệt liên quan đến giao điểm của các đường cao, trung điểm cạnh đáy và điểm cắt đường tròn tại tiếp tuyến từ chân đường cao.