p là số nguyên tố lớn hơn 3

=>p là số lẻ và p không chia hết cho 3

p không chia hết cho 3 nên p=3k+1 hoặc p=3k+2

TH1: p=3k+1

\(25-p^2=25-\left(3k+1\right)^2\)

\(=\left(4-3k-1\right)\left(4+3k+1\right)\)

\(=\left(-3k+3\right)\left(3k+5\right)=-3\left(k-1\right)\left(3k+5\right)⋮3\)(1)

TH2: p=3k+2

\(25-p^2=25-\left(3k+2\right)^2\)

\(=\left(5-3k-2\right)\left(5+3k+2\right)=\left(-3k+3\right)\left(3k+7\right)\)

\(=-3\left(k+1\right)\left(3k+7\right)⋮3\)(2)

Từ (1),(2) suy ra \(25-p^2⋮3\)

p là số lẻ nên p=2k+1

\(25-p^2=25-\left(2k+1\right)^2\)

\(=\left(5-2k-1\right)\left(5+2k+1\right)\)

\(=\left(-2k+4\right)\left(2k+6\right)\)

\(=-4\left(k-2\right)\left(k+3\right)\)

Vì k-2;k+3 có khoảng cách là 5 đơn vị nên (k-2)(k+3)\(⋮\)2

=>\(-4\left(k-2\right)\left(k+3\right)⋮4\cdot2=8\)

=>\(25-p^2⋮8\)

mà \(25-p^2⋮3\)

và ƯCLN(3;8)=1

nên \(25-p^2⋮\left(8\cdot3\right)\)

=>\(25-p^2⋮24\)

Giải:

Theo bài ra ta có:

\(\overline{ba}\) = 2 x \(\overline{ab}\) + 18

10b + a = 20a + 2b + 18

10b - 2b = 20a - a + 18

8b = 19a + 8

8b + 19b = 19b + 19a + 8

27b = 19.(a + b) + 18 (1)

Thay a + b = 9 vào (1)

27b = 19.9 + 18

27b = 171 + 18

27b = 189

b = 189 : 27

b = 7

a = 9 - b

a = 9 - 7

a = 2

Vậy \(\overline{ab}\) = 27

\(x^2+2,5x+5\)

\(=x^2+2\cdot x\cdot\dfrac{5}{4}+\dfrac{25}{16}+\dfrac{55}{16}\)

\(=\left(x+\dfrac{5}{4}\right)^2+\dfrac{55}{16}>=\dfrac{55}{16}>0\forall x\)

=>ĐPCM

Ta có: \(\dfrac{x-1}{3}=\dfrac{x-2}{2}\)

=>3(x-2)=2(x-1)

=>3x-6=2x-2

=>3x-2x=-2+6

=>x=4

Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!

\(x\times\) 2 = 5

\(x=5:2\)

\(x=\frac52\)

Vậy \(x=\frac52\)

X . 2 = 5
X = 5 : 2
X = 2,5

Đổi 5h 24 phút = 27/5 giờ

Gọi độ dài quãng đường AB là x (km) với x>0

Thời gian xe đi từ A đến B là: \(\dfrac{x}{50}\) giờ

Thời gian xe đi từ B về A là: \(\dfrac{x}{40}\) giờ

Tổng thời gian cả đi và về là: \(\dfrac{x}{50}+\dfrac{x}{40}=\dfrac{9x}{200}\) giờ

Do cả đi và về mất 27/5 giờ nên ta có pt:

\(\dfrac{9x}{200}=\dfrac{27}{5}\)

\(\Leftrightarrow x=120\left(km\right)\)

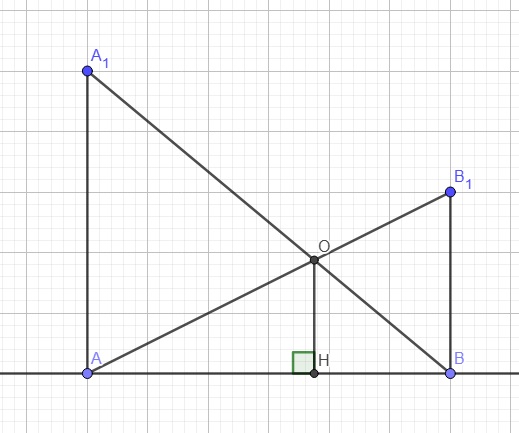
Gọi H là hình chiếu vuông góc của O lên d

\(\Rightarrow AA_1||OH||BB_1\)

Áp dụng định lý Thales trong tam giác \(ABA_1\)

\(\dfrac{OH}{AA_1}=\dfrac{BH}{AB}\)

Áp dụng định lý Thales trong tam giác \(ABB_1\)

\(\dfrac{OH}{BB1}=\dfrac{AH}{AB}\)

\(\Rightarrow\dfrac{OH}{AA_1}+\dfrac{OH}{BB_1}=\dfrac{BH}{AB}+\dfrac{AH}{AB}\)

\(\Rightarrow OH.\left(\dfrac{1}{a}+\dfrac{1}{b}\right)=1\)

\(\Rightarrow OH=\dfrac{a.b}{a+b}\)

Do a, b không đổi \(\Rightarrow OH\) không đổi

Hay khoảng cách từ O đến d không đổi khi A, B chạy trên d