Cháu Hà là người hiếu thảo.

Bích, lớp, cách, toán.

Nghịch ngợm

Giấc ngủ

Vấp ngã

Lắng nghe

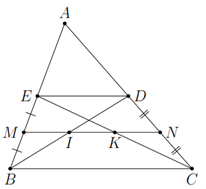
Xét \(\Delta B E D\) có \({\begin{cases}MI//ED\\ ME=BM\end{cases}}\) suy ra \(I D = I B\).

Xét \(\Delta C E D\) có \({}\begin{cases}NK//ED\\ NC=ND\end{cases}\) suy ra \(K E = K C\).

Suy ra \(M I = \frac{1}{2} E D\); \(N K = \frac{1}{2} E D\); \(E D = \frac{1}{2} B C\).

\(I K = M K - M I = \frac{1}{2} B C - \frac{1}{2} D E = D E - \frac{1}{2} D E = \frac{1}{2} D E\).

Vậy \(M I = I K = K N\).

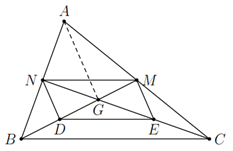
a) Vì \(B M\), \(C N\) là các đường trung tuyến của \(\Delta A B C\) nên \(M A = M C\), \(N A = N B\).

Do đó \(M N\) là đường trung bình của \(\Delta ABC\), suy ra \(M N\) // \(B C\). (1)

Ta có \(D E\) là đường trung bình của \(\Delta GBC\) nên \(D E\) // \(B C\).  (2)

Từ (1) và (2) suy ra \(M N\) // \(D E\).

b) Xét \(\Delta ABG\), ta có \(N D\) là đường trung bình.

Xét \(\Delta ACG\), ta có \(M E\) là đường trung bình.

Do đó \(N D\) // \(A G\), \(M E\) // \(A G\).

Suy ra \(N D\) // \(M E\).

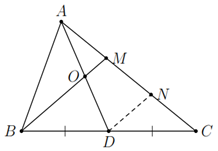
a) Qua \(D\) vẽ một đường thẳng song song với \(B M\) cắt \(A C\) tại \(N\).

Xét \(\Delta MBC\) có \(D B = D C\) và \(D N\) // \(B M\) nên \(M N = N C = \frac{1}{2} M C\) (định lí đường trung bình của tam giác).

Mặt khác \(A M = \frac{1}{2} M C\), do đó \(A M = M N = \frac{1}{2} M C\).

Xét \(\Delta AND\) có \(A M = M N\) và \(B M\) // \(D N\) nên \(O A = O D\) hay \(O\) là trung điểm của \(A D\).

b) Xét \(\Delta AND\) có \(O M\) là đường trung bình nên \(O M = \frac{1}{2} D N\). (1)

Xét \(\Delta MBC\) có \(D N\) là đường trung bình nên \(D N = \frac{1}{2} B M\). (2)

Từ (1) và (2) suy ra \(O M = \frac{1}{4} B M\).

a) Kẻ \(M N\) // \(B D\), \(N \in A C\).

\(M N\) là đường trung bình trong \(\triangle C B D\)

Suy ra \(N\) là trung điểm của \(C D\) (1).

\(I N\) là đường trung bình trong \(\triangle A M N\)

Suy ra \(D\) là trung điểm của \(A N\) (2).

Từ (1) và (2) suy ra \(A D = \frac{1}{2} D C\).

b) Có \(I D = \frac{1}{2} M N\); \(M N = \frac{1}{2} B D\), nên \(B D = I D\).

a) Tứ giác \(A E D F\) có \(\hat{E A F} = \hat{A E D} = \hat{A F D} = 90^{\circ}\) nên là hình chữ nhật.

\(\Delta A B C\) vuông cân tại \(A\) có \(A M\) là trung tuyến nên \(A M\) cũng là đường phân giác \(\hat{E A F}\).

Hình chữ nhật \(A E D F\) có đường chéo \(A D\) là tia phân giác \(\hat{E A F}\) nên là hình vuông.

b) \(\Delta A E F\) vuông tại \(A\) có \(A E = A F\) nên vuông cân tại \(A\)

Suy ra \(\hat{F_{1}} = 45^{\circ} = \hat{C}\) mà \(\hat{F_{1}} , \hat{C}\) đồng vị nên \(E F\) // \(B C .\)

c) Gọi \(O\) là giao của \(A D\) với \(E F\) suy ra \(O E = O D = O F = O A\)

\(\Delta E N F\) vuông tại \(N\) có \(N O\) là đường trung tuyến nên \(N O = E O = F O\)

\(\Delta A N D\) có \(N O\) là đường trung tuyến mà \(N O = \frac{A D}{2}\) suy ra \(\Delta A N D\) vuông tại \(N .\)

a) Tứ giác \(A D M E\) có \(\hat{D A E} = \hat{D} = \hat{E} = 90^{\circ}\) nên \(A D M E\) là hình chữ nhật.

b) Vì \(D M ⊥ A B\) và \(A C ⊥ A B\) nên \(D M\) // \(A C\) suy ra \(\hat{C} = \hat{B M D}\) (so le trong).

Xét \(\Delta D M B\) và \(\Delta E C M\) có:

     \(\hat{D} = \hat{E} = 90^{\circ}\)

     \(B M = C M\) (giả thiết)

     \(\hat{D M B} = \hat{C}\) (so le trong)

Vậy \(\Delta D M B = \Delta E C M\) (cạnh huyền - góc nhọn)

Suy ra \(M E = B D\) (hai cạnh tương ứng) mà \(M E = A D\) nên \(A D = B D\).

Tứ giác \(A M B I\) có hai đường chéo \(A B , M I\) cắt nhau tại \(D\) là trung điểm của mỗi đường nên là hình bình hành.

Mà \(M I ⊥ A B\) suy ra \(A M B I\) là hình thoi.

c) Để \(A M B I\) là hình vuông thì \(A M ⊥ B M\) hay \(A M\) vừa là đường trung tuyến vừa là đường cao nên \(\Delta A B C\) vuông cân tại \(A .\)

d) Giả sử \(A M\) cắt \(P Q\) tại \(F\) và \(P Q\) cắt \(A H\) tại \(O\).

Khi đó \(\Delta O A Q\) có \(O A = O Q\) nên \(\&\text{nbsp}; \Delta O A Q\) cân tại \(O\) suy ra \(\hat{Q_{1}} = \hat{O A Q}\)

\(\Delta A M C\) cân tại \(M\) suy ra \(\hat{A_{1}} = \hat{C}\)

Do đó, \(\hat{A_{1}} + \hat{Q_{1}} = \hat{C} + \hat{O A Q} = 90^{\circ}\)

Suy ra \(\Delta F A Q\) vuông tại \(F\) hay \(A M ⊥ P Q .\)

a) Tứ giác \(A B C D\) có hai đường chéo \(A C , B D\) cắt nhau tại trung điểm \(N\) của mỗi đường nên là hình bình hành.

b) Ta có \(A P ⊥ B C\); \(A Q\) // \(B C\) suy ra \(A P ⊥ A Q\).

Tứ giác \(A P C Q\) có ba góc vuông nên là hình chữ nhật.

Khi đó hai đường chéo \(A C , P Q\) cắt nhau tại trung điểm của mỗi đường, mà \(N A = N C\) nên \(N\) là trung điểm của \(P Q\).

Suy ra \(P , N , Q\) thẳng hàng.

c) Để tứ giác \(A B C D\) là hình vuông thì ta cần \(A B ⊥ B C , A B = B C\) hay \(\Delta A B C\) vuông cân tại \(B .\)