Ta có \(V T = \frac{\frac{4 x^{2}}{y^{2}}}{\left(\left(\right. \frac{x^{2}}{y^{2}} + 1 \left.\right)\right)^{2}} + \frac{x^{2}}{y^{2}} + \frac{y^{2}}{x^{2}}\)

Đặt \(\frac{x^{2}}{y^{2}} = t \left(\right. t > 0 \left.\right)\) thì VT thành

\(\frac{4 t}{\left(\left(\right. t + 1 \left.\right)\right)^{2}} + t + \frac{1}{t}\)

\(= \frac{4 t}{\left(\left(\right. t + 1 \left.\right)\right)^{2}} + \frac{t^{2} + 1}{t}\)

\(= \frac{4 t}{\left(\left(\right. t + 1 \left.\right)\right)^{2}} + \frac{\left(\left(\right. t + 1 \left.\right)\right)^{2}}{t} - 2\)

Đặt \(\frac{\left(\left(\right. t + 1 \left.\right)\right)^{2}}{t} = u \left(\right. u \geq 4 \left.\right)\) (vì BĐT \(\left(\left(\right. a + b \left.\right)\right)^{2} \geq 4 a b\))

Khi đó \(V T = u + \frac{4}{u} - 2\)

 \(= \frac{4}{u} + \frac{u}{4} + \frac{3 u}{4} - 2\)

\(\geq 2 \sqrt{\frac{4}{u} . \frac{u}{4}} + \frac{3.4}{4} - 2\)

\(= 2 + 3 - 2\)

\(= 3\)

\(\Rightarrow V T \geq 3\)

Dấu "=" xảy ra \(\Leftrightarrow u = 4\) \(\Leftrightarrow t = 1\) \(\Leftrightarrow x = \pm y\)

Vậy ta có đpcm. Dấu "=" xảy ra \(\Leftrightarrow x = \pm y\)

a,Ta có: đường cao AH 

=> AH vuông góc BC => AHB = 90`

Tam giác ABC vuông tại A

=> ABC = 90`

Xét hai tam giác ABC và HBA có:

• AHB = ABC (=90`)
• chung góc B

=>    Δ ABC ~ Δ HBA (g-g)

=> \(\frac{A B}{H B} = \frac{B C}{B A}\) ( các cạnh tưng ứng )

​=> AB.BA=HB.BC \(A B^{2}\) = BC.BH

​Vậy ΔABC ~ ΔHBA ; \(A B^{2}\)= BC.BH

Gọi quãng đường AB là: \(x \left(\right. k m , x > 0 \left.\right)\)

Vận tốc trung bình là 15km/h nên vận tốc lúc về là: \(2 \cdot 15 - 12 = 18 \left(\right. k m / h \left.\right)\)

Thời gian đi là: \(\frac{x}{12} \left(\right. h \left.\right)\)

Thời gian về là: \(\frac{x}{18} \left(\right. h \left.\right)\)

Lúc về nhiều hơn lúc đi 45 phút ta có phương trình:

\(\frac{x}{12} - \frac{x}{18} = \frac{3}{4}\) 

\(\Leftrightarrow x \left(\right. \frac{1}{12} - \frac{1}{18} \left.\right) = \frac{3}{4}\)

\(\Leftrightarrow x \cdot \frac{1}{36} = \frac{3}{4}\)

\(\Leftrightarrow x = \frac{3}{4} : \frac{1}{36}\)

\(\Leftrightarrow x = 27 \left(\right. k m \left.\right)\)

x2−93x+15​+x+31​−x−32​=(x−3)⋅(x+3)3⋅(x+5)​+x+31​−x−32​=(x−3)⋅(x+3)3⋅(x+5)​+(x+3)⋅(x−3)x−3​−(x−3)⋅(x+3)2⋅(x+3)​\(= \frac{3 \cdot \left(\right. x + 5 \left.\right) + x - 3 - 2 \cdot \left(\right. x + 3 \left.\right)}{\left(\right. x - 3 \left.\right) \cdot \left(\right. x + 3 \left.\right)} = \frac{3 x + 15 + x - 3 - 2 x - 6}{\left(\right. x - 3 \left.\right) \cdot \left(\right. x + 3 \left.\right)} = \frac{2 x + 6}{\left(\right. x + 3 \left.\right) \cdot \left(\right. x - 3 \left.\right)} = \frac{2 \cdot \left(\right. x + 3 \left.\right)}{\left(\right. x + 3 \left.\right) \cdot \left(\right. x - 3 \left.\right)} = \frac{2}{x - 3}\)

câu b

để \(\frac{2}{x - 3} = \frac{2}{3}\) thì \(x - 3 = 3\)

\(\Rightarrow x = 3 + 3 = 6\)

vậy  \(x = 6\) thì \(A = \frac{2}{3}\)

Nửa chu vi tam giác:

\(\frac{\left(\right. 10 + 17 + 21 \left.\right)}{2} = 24 \left(\right. c m \left.\right)\)

Diện tích tam giác:

\(S = \sqrt{24. \left(\right. 24 - 10 \left.\right) . \left(\right. 24 - 17 \left.\right) . \left(\right. 24 - 21 \left.\right)} = 84 \left(\right. c m^{2} \left.\right)\)'

Chiều cao của mỗi hình chóp tứ giác đều là:

     30:2=1530:2=15 (m).

Thể tích của lồng đèn quả trám là:

     𝑉=2.(13.20.20.15)=4000V=2.(31​.20.20.15)=4000 (cm33).

Gọi A là biến cố "Lấy được viên bi màu đỏ"

Trong túi có 8 viên màu đỏ nên n(A)=8

=>\(P \left(\right. A \left.\right) = \frac{8}{19}\)

1: 

a: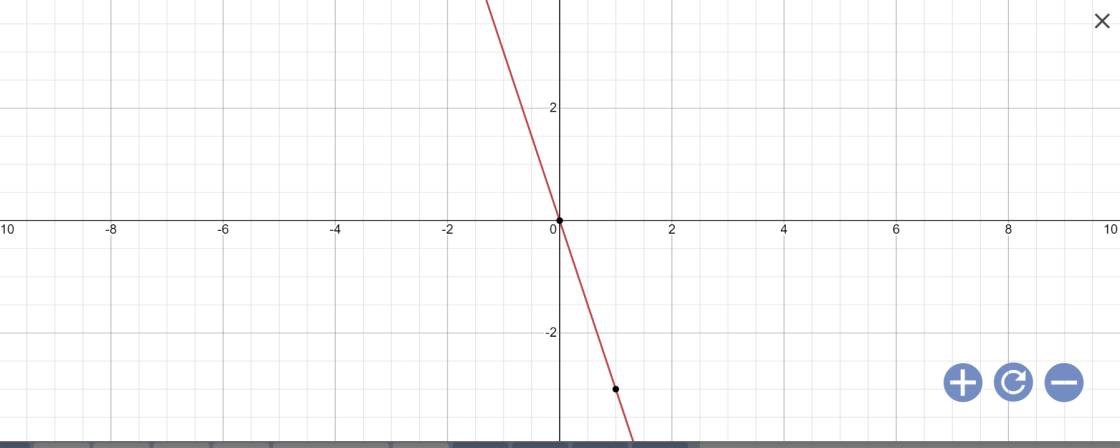 

b: Vì (d3)//(d2) nên \(\left{\right. a = 1 \\ b \neq 2\)

Vậy: (d3): y=x+b

Thay x=-1 và y=3 vào (d3), ta được:

b-1=3

=>b=4

Vậy: (d3): y=x+4

Bài 2:

Gọi số sản phẩm tổ 1 phải sản xuất theo kế hoạch là x(sản phẩm)

(ĐIều kiện: \(x \in Z^{+}\))

Số sản phẩm tổ 2 phải sản xuất theo kế hoạch là:

900-x(sản phẩm)

Số sản phẩm thực tế tổ 1 làm được là:

\(x \left(\right. 1 + 20 \% \left.\right) = 1 , 2 x \left(\right. s ả n p h ẩ m \left.\right)\)

Số sản phẩm thực tế tổ 2 làm được là:

\(\left(\right. 900 - x \left.\right) \left(\right. 1 + 15 \% \left.\right) = 1 , 15 \left(\right. 900 - x \left.\right) \left(\right. s ả n p h ẩ m \left.\right)\)

Tổng số sản phẩm là 1055 sản phẩm nên ta có:

1,2x+1,15(900-x)=1055

=>0,05x+1035=1055

=>0,05x=20

=>x=400(nhận)

Vậy: số sản phẩm tổ 1 phải sản xuất theo kế hoạch là 400 sản phẩm

số sản phẩm tổ 2 phải sản xuất theo kế hoạch là 900-400=500 sản phẩm

a) \(2 x = 7 + x\)

\(\Leftrightarrow 2 x - x = 7\)

\(\Leftrightarrow x = 7\)

Vậy \(S = \left{\right. 7 \left.\right}\)

b) \(\frac{x - 3}{5} + \frac{1 + 2 x}{3} = 6\)

\(\Leftrightarrow \frac{3 \left(\right. x - 3 \left.\right)}{15} + \frac{5 \left(\right. 1 + 2 x \left.\right)}{15} = 6\)

\(\Leftrightarrow \frac{3 x - 9 + 5 + 10 x}{15} = 6\)

\(\Leftrightarrow 13 x - 4 = 90\)

\(\Leftrightarrow 13 x = 94\)

\(\Leftrightarrow x = \frac{94}{13}\)

Vậy \(S = \left{\right. \frac{94}{13} \left.\right}\).

1 I think robots can't replace the role of teachers in education

2 People will still send letters to each other in 2050