a) Các trường hợp thuyết trình theo thứ tự 1, 2, 3 có thể xảy ra là:

ABC, ACB, BAC, BCA, CAB, CBA

b)

+) Từ câu a) ta thấy có tất cả 6 kết quả

+) Ngoài cách đếm ta có thể sử dụng quy tắc nhân để tìm kết quả

Kết quả bốc thăm thuyết trình gồm 3 công đoạn

Công đoạn 1: Bốc thăm xác định đội trình bày đầu tiên, có thể xảy ra 3 kết quả (A, B hoặc C)

Công đoạn 2: Bốc thăm xác định đội trình bày thứ 2, có thể xảy ra 2 kết quả (trừ 1 đội đã thuyết trình đầu tiên

Công đoạn 3: Đội trình bày cuối cùng chỉ có thể duy nhất là đội còn lại

Áp dụng quy tắc nhân, ta tìm được số kết quả có thể xảy ra là:

                             \(3.2.1 = 6\) (cách)

Viên bi màu trắng

bài này lp mí z

`\Omega_1=C_9 ^1=9`

`\Omega_2=C_13 ^2=78`

`@TH1:`

Gọi `A:`"Lấy từ hộp thứ nhất viên bi trắng."

   `=>A=C_5 ^1=5`

   `=>P(A)=5/9`

Gọi `B:`" Lấy từ hộp thứ hai `2` viên bi trắng."

   `=>B=C_8 ^2=28`

  `=>P(B)=5/9 . 28/78=70/351`

`@TH2:`

Gọi `C:`"Lấy từ hộp thứ nhất viên bi xanh."

    `=>C=C_4 ^1=4`

        `=>P(C)=4/9`

Gọi `D:`" Lấy từ hộp thứ hai `2` viên bi trắng."

    `=>D=C_7 ^2=21`

         `=>P(D)=4/9 . 21/78=14/117`

 Do nếu thực hiện 1 thao tác thì số bi trong mỗi chồng vẫn không thay đổi nên chắc chắn trong số các chồng ban đầu phải có đúng 1 chồng chứa 1 viên bi. (Vì nếu chồng nào cũng có từ 2 viên bi trở lên thì sau khi thực hiện thao tác, ta sẽ có thêm 1 cột mới, không thỏa mãn; còn nếu có 2 hay nhiều chồng có 1 viên bi thì sau khi thực hiện thao tác, số chồng sẽ giảm đi.)

 Hơn nữa, lập luận tương tự, sau khi thực hiện xong thao tác lần đầu, ở lần thứ hai cũng bắt buộc phải có đúng một chồng có 1 viên bi. Điều này đòi hỏi ban đầu phải có đúng 1 chồng có 2 viên bi.

 Cứ tiếp tục như thế, trong số các chồng ban đầu, phải có 1 chồng có 3 viên và 1 chồng có 4 viên bi. Do đó, chỉ có duy nhất 1 trường hợp sau là thỏa mãn ycbt. 

Vậy có thể có 4 cọc tất cả.

Có tổng cộng 6 cách là:

1 ng thuộc tổ 1 và 1 ng thuộc tổ 2

1 ng thuộc tổ 1 và 1 ng thuộc tổ 3

1 ng thuộc tổ 1 và 1 ng thuộc tổ 4

1 ng thuộc tổ 2 và 1 ng thuộc tổ 3

1 ng thuộc tổ 2 và 1 ng thuộc tổ 4

1 ng thuộc tổ 3 và 1 ng thuộc tổ 4

Tham khảo:

a) Đổi: 1 giờ 30 phút = 1,5 giờ; 15 phút = 0,25 giờ; t phút = \(\frac{t}{{60}}\) giờ

Nếu \(t \le 90\)(phút) thì quãng đường s mà người đó đi được là: \(42.\frac{t}{{60}} = 0,7t\)(km)

Nếu \(90 < t \le 90 + 15 = 105\)(phút) thì quãng đường s mà người đó đi được là: \(42.1,5 = 63\)(km)

Nếu \(105 < t \le 105 + 120 = 225\)(phút) thì quãng đường s mà người đó đi được là: \(42.1,5 + (\frac{t}{{60}} - 1,5 - 0,25).30 = 0,5t + 10,5.\)(km)

Như vậy hàm số tính quãng đường s (km) sau t phút là:

\(s = \left\{ \begin{array}{l}0,7t\quad \quad \quad \quad (0 \le t \le 90)\\63\quad \quad \quad \quad \;\;\;(90 < t \le 105)\\0,5t + 10,5\quad \;\;(105 < t \le 225)\end{array} \right.\)

b)

Với \(0 \le t \le 90\) thì \(s = 0,7t\)

Trên đoạn [0;90] ta vẽ đường thẳng \(s = 0,7t\)

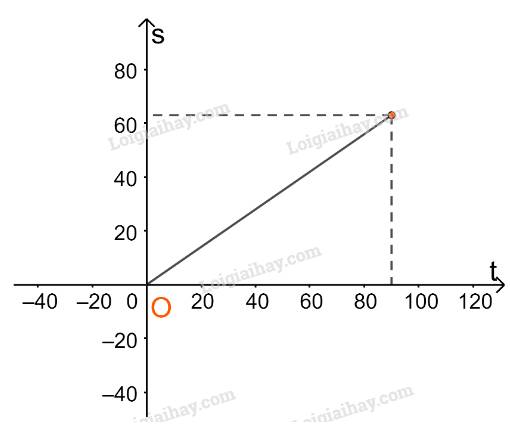
Với \(90 < t \le 105\) thì \(s = 63(km)\)

Trên nửa khoảng (90;105] ta vẽ đường thẳng \(s = 63\)

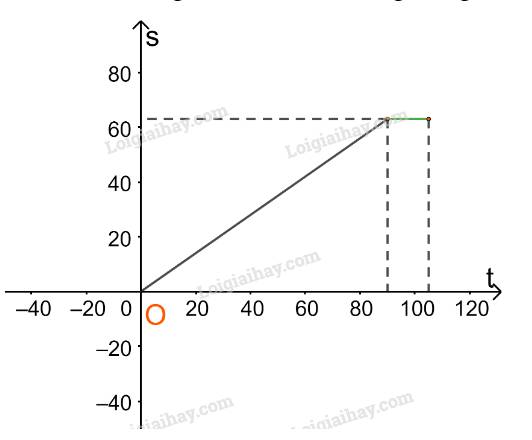
Với \(105 < t \le 225\)(phút) thì \(s = 0,5t + 10,5.\)(km)

Trên nửa khoảng (105;225] ta vẽ đường thẳng \(s = 0,5t + 10,5.\)

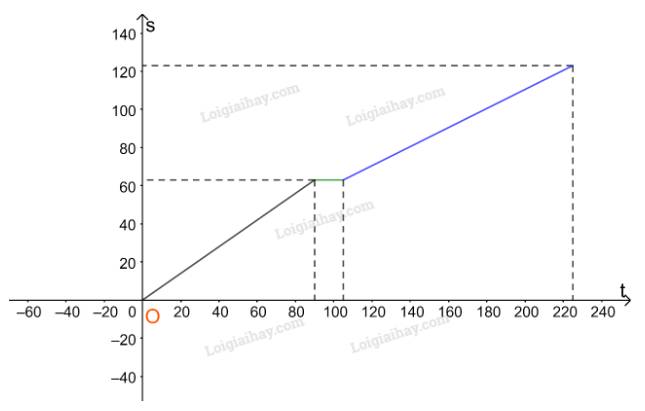
Như vậy ta được đồ thị biểu diễn hàm số s theo t như hình trên.

a)

Do x là số lượng khách thứ 51 trở lên nên x>0.

Cứ thêm 1 người thì giá còn (300000-5 000.1) đồng/người cho toàn bộ hành khách.

Thêm x người thì giá còn (300 000-5 000.x) đồng/người cho toàn bộ hành khách.

Doanh thu theo x: \(\left( {50 + x} \right).\left( {300000 - 5000x} \right)\) (VNĐ)

b) Do chi phí thực sự cho chuyến đi là 15 080 000 đồng nên để công ty không bị lỗ thì doanh thu phải lớn hơn hoặc bằng 15 080 000 đồng

Khi đó:

\(\begin{array}{l}\left( {50 + x} \right).\left( {300000 - 5000x} \right) \ge 15080000\\ \Leftrightarrow \left( {50 + x} \right).5000.\left( {60 - x} \right) \ge 15080000\\ \Leftrightarrow \left( {x + 50} \right)\left( {60 - x} \right) \ge 3016\\ \Leftrightarrow  - {x^2} + 10x + 3000 \ge 3016\\ \Leftrightarrow  - {x^2} + 10x - 16 \ge 0\\ \Leftrightarrow {x^2} - 10x + 16 \le 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {x - 8} \right) \le 0\\ \Leftrightarrow 2 \le x \le 8\end{array}\)

Vậy số người của nhóm du khách nhiều nhất là 58 người.

a)

Gọi x là số lượng khách từ người thứ 11 trở lên của nhóm (x>0)

Giá vé khi có thêm x khách là: \(800{\rm{ }}000 - 10{\rm{ }}000.x\)(đồng/người)

Doanh thu khi thêm x khách là:

\(\left( {x + 10} \right).\left( {800000 - 10000x} \right)\)\( = 10000\left( {x + 10} \right)\left( {80 - x} \right)\) (đồng)

b)

Chi phí thực sau khi thêm x vị khách là: 700 000(x+10) (đồng)

Lợi nhuận khi thêm x vị khách là:

\(T = 10000\left( {x + 10} \right)\left( {80 - x} \right)\)\( - 700000\left( {x + 10} \right)\)

\(\begin{array}{l} = 10000\left( {x + 10} \right).\left[ {80 - x - 70} \right]\\ = 10000\left( {x + 10} \right)\left( {10 - x} \right)\end{array}\)

Để công ty không bị lỗ thì lợi nhuận lớn hơn hoặc bằng 0

\(\begin{array}{l} \Leftrightarrow 10000\left( {x + 10} \right)\left( {10 - x} \right) \ge 0\\ \Leftrightarrow  - 10 \le x \le 10\end{array}\)

Khi đó số khách du lịch tối đa là \(x + 10 = 10 + 10 = 20\) người thì công ty không bị lỗ.