Olm chào em, cảm ơn đánh giá mười sao của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!

\(x-2xy-1=x\left(5-x\right)-\left(y+20\right)\)

\(\Leftrightarrow x-2xy-1=5x-x^2-y-20\)

\(\Leftrightarrow x^2-4x+19=2xy-y\)

\(\Leftrightarrow x^2-4x+19=y\left(2x-1\right)\)

\(\Leftrightarrow y=\dfrac{x^2-4x+19}{2x-1}\) (1)

\(\Leftrightarrow4y=\dfrac{4x^2-16x+76}{2x-1}\)

\(\Leftrightarrow4y=2x-7+\dfrac{69}{2x-1}\)

Do x;y nguyên nên \(4y\) và \(2x-7\) nguyên

\(\Rightarrow\dfrac{69}{2x-1}\in Z\)

\(\Rightarrow2x-1\inƯ\left(69\right)=\left\{-69;-23;-3;-1;1;3;23;69\right\}\)

\(\Rightarrow x\in\left\{-34;-11;-1;0;1;2;12;35\right\}\)

Thế  lần lượt vào (1) được tương ứng \(y\in\left\{-19;-8;-8;-19;-19;16;5;5;16\right\}\)

Vậy ...

\(C\left(x\right)=4-2x+\left(x+2\right)=0\)

\(4-2x+x+2=0\)

\(6-x=0\)

\(x=6\)

Vậy nghiệm đa thức là x=6

H(\(x\)) = 3 - \(x^2\)

H(\(x\)) = 0 khi và chỉ khi:

3 - \(x^2\) = 0

\(x^2=3\)

\(\left[\begin{array}{l}x=-\sqrt3\\ x=\sqrt3\end{array}\right.\)

Vậy H(\(x\)) có hai nghiệm là: -\(\sqrt3\); \(\sqrt3\)

35 x 4 : 1 + 100 : 35 : 6 : 5 + 34

= 140 : 1 + \(\frac{20}{7}\) : 6 : 5 + 34

= 140 + \(\frac{10}{21}\) : 5 + 34

= (140 + 34) + \(\frac{2}{21}\)

= 174 + \(\frac{2}{21}\)

= \(\frac{3654}{21}\) + \(\frac{2}{21}\)

= \(\frac{3656}{21}\)

Giải:

Nếu y tỉ lệ nghịch với x theo tỉ lệ là a thì x cũng tỉ lệ với y theo hệ số tỉ lệ là a

a.

\(H\left(x\right)=A\left(x\right)+B\left(x\right)\)

\(H\left(x\right)=x^4+3x^3-5x^2+7x+\left(-x^4\right)-3x^3+5x^2+7\)

\(H\left(x\right)=7x+7\)

b.

\(K\left(x\right)=A\left(x\right)-B\left(x\right)\)

\(K\left(x\right)=x^4+3x^3-5x^2+7x-\left(-x^4-3x^3+5x^2+7\right)\)

\(K\left(x\right)=2x^4+6x^3-10x^2+7x-7\)

c.

\(H\left(x\right)=7x+7=0\)

\(7x=-7\)

\(x=-1\)

Vậy nghiệm của H(x) là \(x=-1\)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

Do đó: ΔAHB=ΔAHC

b: ΔAHB=ΔAHC

=>\(\widehat{HAB}=\widehat{HAC}\)

=>AH là phân giác của góc BAC

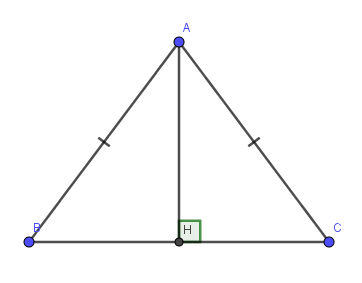
a) Xét hai tam giác vuông: \(\Delta AHB\) và \(\Delta AHC\) có:

\(AB=AC\left(gt\right)\)

\(AH\) là cạnh chung

\(\Rightarrow\Delta AHB=\Delta AHC\) (cạnh huyền - cạnh góc vuông)

b) Do \(\Delta AHB=\Delta AHC\left(cmt\right)\)

\(\Rightarrow\widehat{BAH}=\widehat{CAH}\) (hai góc tương ứng)

\(\Rightarrow AH\) là tia phân giác của \(\widehat{BAC}\)

Giải:

(\(x-3\))\(^5\) = 4.(\(x-3\))\(^3\)

(\(x-3\))\(^5\) - 4.(\(x-3\))\(^3\) = 0

(\(x-3\))\(^3\).[(\(x-3)^2\) - 4] = 0

\(\left[\begin{array}{l}x-3=0\\ \left(x-3\right)^2=4\end{array}\right.\)

\(\left[\begin{array}{l}x=3\\ x-3=-2\\ x-3=2\end{array}\right.\)

\(\left[\begin{array}{l}x=3\\ x=-2+3\\ x=2+3\end{array}\right.\)

\(\left[\begin{array}{l}x=3\\ x=1\\ x=5\end{array}\right.\)

Vậy \(x\in\left\lbrace1;3;5\right\rbrace\)

(x - 3)⁵ = 4(x - 3)³

(x - 3)⁵ - 4(x - 3)³ = 0

(x - 3)³.[(x - 3)² - 4] = 0

(x - 3)³.(x - 3 - 2)(x - 3 + 2) = 0

(x - 3)³(x - 5)(x - 1) = 0

(x - 3)³ = 0 hoặc x - 5 = 0 hoặc x - 1 = 0

*) (x - 3)³ = 0

x - 3 = 0

x = 3

*) x - 5 = 0

x = 5

*) x - 1 = 0

x = 1

Vậy x = 1; x = 3; x = 5

a: Bảng tần số:

Tần số tương ứng của giá trị 32 là \(\dfrac{6}{20}=30\%\)

=>Sai

b: Sai

c: Sai

d: Sai