Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Diện tích xung quanh của hình chóp tam giác đều là: \(\frac{{10.3}}{2}.12 = 180\) (\(c{m^2}\))
b) Diện tích xung quanh của hình chóp tứ giác đều là: \(\frac{{72.4}}{2}.77 = 11088\) (\(d{m^2}\))
Diện tích đáy của hình chóp tứ giác đều là: \({72^2}=5184\) (\(d{m^2}\))
Diện tích toàn phần của hình chóp tứ giác đều là: \(11088 + 5184 = 16 272\) (\(d{m^2}\))
Thể tích của hình chóp tứ giác đều là: \(\frac{1}{3}.5184.68,1=117676,8\) (\(d{m^3}\))

Hình chóp tam giác đều nên là chiều cao của mặt bên xuất phát từ đỉnh chính là trung đoạn
Sxq=1/2*10*3*12=5*36=180cm2

a) Diện tích xung quanh của hình chóp tam giác đều là:
\(\frac{{99.40}}{2}.3 = 5940\) (\(c{m^2}\))
Diện tích đáy của hình chóp là:
\(\frac{{40.34,6}}{2} = 692\) (\(c{m^2}\))
Diện tích toàn phần của hình chóp là:
\(5940 + 692 = 6632\) (\(c{m^2}\))
Thể tích của hình chóp là:
\(\frac{1}{3}.692.98,3 \approx 22674,53\) (\(c{m^3}\))
b) Diện tích xung quanh của hình chóp tứ giác đều là:
\(\frac{{91.120}}{2}.4 = 21840\) (\(c{m^2}\))
Diện tích đáy của hình chóp là:
\(120.120 = 14400\) (\(c{m^2}\))
Diện tích toàn phần của hình chóp là:
\(21840 + 14400 = 36240\) (\(c{m^2}\))
Thể tích của hình chóp là:
\(\frac{1}{3}.14400.68,4 = 328320\) (\(c{m^3}\))

a: Sxq=1/2*2,2*2,5*4=11m2
b: Diện tích cần làm mái che là: 11+2,5^2=17,25m2
Số tiền cần chi là:
17,25*2000000=34500000(đồng)

a: Chu vi đáy là 20*3=60(cm)
Diện tích xung quanh là \(17.32\cdot60=1039.2\left(cm^2\right)\)
b: Chu vi đáy là \(4\cdot3=12\left(cm\right)\)
Diện tích đáy là \(\dfrac{1}{2}\cdot3.5\cdot4=7\left(cm^2\right)\)
Diện tích xung quanh là \(12\cdot5=60\left(cm^2\right)\)
Diện tích toàn phần là \(60+7=67\left(cm^2\right)\)

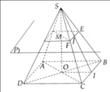
a) Gọi O là tâm của đáy ABCD, M là giao điểm của SO và mặt phẳng (P). Ta có: OM = 2(cm).
Ta tính được O B = 2 2 c m rồi suy ra SO = 5 (cm)
Từ đó chiều cao cần tìm là: SM = SO - OM 3 (cm)
b) Gọi I là trung điểm của BC. E, F, J lần lượt là giao điểm của SB, SC, SI với mặt phẳng (p).
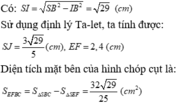

Gọi \(a\) là cạnh đáy hình chóp tứ giác đều \(\left(cm\right)\)
\(h\) là chiều cao hình chóp tứ giác đều \(\left(cm\right)\)
\(d\) là trung đoạn\(\left(cm\right)\)
Ta có :
\(S_{xq}=4S=4.\dfrac{1}{2}a.d=2ad\)
mà \(d^2=h^2+\dfrac{a^2}{4}\Rightarrow d=\sqrt[]{h^2+\dfrac{a^2}{4}}\)
\(\Rightarrow S_{xq}=2a\sqrt[]{h^2+\dfrac{a^2}{4}}\)
\(\Leftrightarrow S^2_{xq}=4a^2\left(h^2+\dfrac{a^2}{4}\right)=4a^2h^2+a^4\)
\(\Leftrightarrow a^4+4a^2h^2-S^2_{xq}=0\)
\(\Leftrightarrow a^4+4a^2.36-36^2=0\)
\(\Leftrightarrow a^4+144a^2-1296=0\left(1\right)\)
\(\Delta'=5184+1296=6480\Rightarrow\sqrt[]{\Delta'}=36\sqrt[]{5}\)
Pt (1) có nghiệm \(a^2=-72+36\sqrt[]{5}=36\left(1-\sqrt[]{5}\right)\)
\(\)\(\Rightarrow a=6\sqrt[]{1-\sqrt[]{5}}\left(cm\right)\) (cạnh đáy là hình vuông)
Vậy cạnh đáy tứ giác đều là \(a=6\sqrt[]{1-\sqrt[]{5}}\left(cm\right)\)
Đính chính
\(...a^2=-72+36\sqrt[]{2}=36\left(\sqrt[]{5}-2\right)\)
\(\Rightarrow a=6\sqrt[]{\sqrt[]{5}-2}\left(cm\right)\)
Vậy cạnh tứ giác đều là \(a=6\sqrt[]{\sqrt[]{5}-2}\left(cm\right)\)


Ta có cạnh đáy tam giác đều là 60 cm, cạnh bên là 96,4 cm.
Chiều cao của một mặt bên là:
\(h = \sqrt{96,4^{2} - 30^{2}} = \sqrt{9291,76 - 900} = \sqrt{8391,76} \approx 91,6 \&\text{nbsp};\text{cm}\)
Diện tích một mặt bên:
\(S = \frac{1}{2} \times 60 \times 91,6 = 30 \times 91,6 = 2748 \&\text{nbsp}; \text{cm}^{2}\)
Diện tích xung quanh hình chóp là:
\(3 \times 2748 = 8244 \&\text{nbsp}; \text{cm}^{2}\)
Vậy diện tích xung quanh hình chóp là 8244 cm²
Đáy là tam giác đều có cạnh dài 60 cm, nên chu vi đáy là:
3 × 60 = 180 cm
Chiều cao mặt bên đã được cho là l = 96,4 cm
Diện tích xung quanh hình chóp là :
\(\frac12\) x 180 x 96,4 = 8676 \(\operatorname{cm}^2\)